UP Board Solutions for Class 9 Maths Chapter 1 Number systems (संख्या पद्धति)
These Solutions are part of UP Board Solutions for Class 9 Maths. Here we have given UP Board Solutions for Class 9 Maths Chapter 1 Number systems (संख्या पद्धति).
प्रश्नावली 1.1
प्रश्न 1.
क्या शून्य एक परिमेय संख्या है? क्या आप इसे के रूप में लिख सकते हैं जहाँ p और q पूर्णाक हैं और q ≠ 0 है?
हल :
हाँ, शून्य एक परिमेय संख्या है।
इसे ![]() के रूप में लिखा जा सकता है।
के रूप में लिखा जा सकता है।
0 = ![]() ,
, ![]() ,
, ![]() ,……….
,……….
प्रश्न 2.
3 और 4 के मध्य 6 परिमेय संख्याएँ ज्ञात कीजिए।
हल :
6 परिमेय संख्याएँ ज्ञात करने के लिए, 3 और 4 को (6 + 1) = 7 से गुणा और भाग करते हैं।
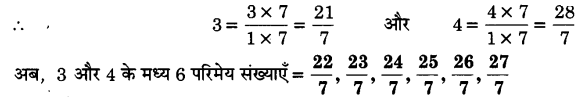
प्रश्न 3.
और
के बीच पाँच परिमेय संख्याएँ ज्ञात कीजिए।
हल :
चूँकि दी गई परिमेय संख्याओ का हर समान है।
पाँच परिमेय संख्याएँ ज्ञात करने के लिए, और
को (5 + 1) = 6 से गुणा और भाग करते हैं।

प्रश्न 4.
नीचे दिए गए कथन सत्य हैं या असत्य? कारण के साथ अपने उत्तर दीजिए :
(i) प्रत्येक प्राकृत संख्या एक पूर्ण संख्या होती है।
(ii) प्रत्येक पूर्णाक एक पूर्ण संख्या होती है।
(iii) प्रत्येक परिमेय संख्या एक पूर्ण संख्या होती है।
हल :
(i) क्योंकि सभी प्राकृत संख्याएँ {1, 2, 3, 4, ….}, पूर्ण संख्याओं {0, 1, 2, 3, 4, ….} में समाहित हैं। अतः कथन सत्य है।
(ii) क्योंकि ऋणात्मक पूर्णाक, पूर्ण संख्याओं में समाहित नहीं है। अतः कथन असत्य है।
(iii) क्योंकि परिमेय संख्याओं के संग्रह में भिन्ने एवं दशमलव संख्याएँ होती हैं जो पूर्ण संख्याओं के संग्रह में समाहित नहीं हैं। अतः कथन असत्य है।
प्रश्नावली 1.2
प्रश्न 1.
नीचे दिए गए कथन सत्य हैं या असत्य? कारण के साथ अपने उत्तर दीजिए :
(i) प्रत्येक अपरिमेय संख्या एक वास्तविक संख्या होती है।
(ii) संख्या रेखा का प्रत्येक बिन्दु √m के रूप का होता है जहाँ m एक प्राकृत संख्या है।
(iii) प्रत्येक वास्तविक संख्या एक अपरिमेय होती है।
हल :
(i) क्योंकि वास्तविक संख्याओं का संग्रह परिमेय और अपरिमेय संख्याओं से मिलकर बना है अतः प्रत्येक अपरिमेय संख्या वास्तविक होती है। अत: कथन सत्य है।
(ii) यदि m एक प्राकृतिक संख्या है तो संख्या रेखा पर केवल 1, 2, 3, 4,……. बिन्दु ही स्थित होने चाहिए।
जबकि संख्या रेखा पर दो क्रमिक संख्याओं के मध्य अनन्त “संख्याएँ होती हैं। अत: कथन असत्य है।
(iii) क्योंकि वास्तविक संख्याओं के संग्रह में परिमेय और अपरिमेय दोनों प्रकार की संख्याएँ होती हैं। अत: प्रत्येक वास्तविक संख्या का अपरिमेय होना आवश्यक नहीं है। अतः कथन असत्य है।
प्रश्न 2.
क्या सभी धनात्मक पूर्णांकों के वर्गमूल अपरिमेय होते हैं? यदि नहीं, तो एक ऐसी संख्या के वर्गमूल का उदाहरण दीजिए जो एक परिमेय संख्या है।
हल :
नहीं, सभी धनात्मक पूर्णांकों के वर्गमूल अपरिमेय नहीं होते हैं।
उदाहरणार्थ : √9 = 3 एक परिमेय संख्या है।
प्रश्न 3.
दिखाइए कि संख्या रेखा पर √5 को किस प्रकार निरूपित किया जा सकता है?

प्रश्नावली 1.3
प्रश्न 1.
निम्नलिखित भिन्नों को दशमलव रूप में लिखिए और बताइए कि प्रत्येक को दशमलव प्रसार किस प्रकार का है :





प्रश्न 3.
निम्नलिखित को ![]() के रूप में व्यक्त कीजिए, जहाँ p और q पूर्णाक है तथा q ≠ 0 है :
के रूप में व्यक्त कीजिए, जहाँ p और q पूर्णाक है तथा q ≠ 0 है :


प्रश्न 4.
0.99999…. को के रूप में व्यक्त कीजिए। क्या आप अपने उत्तर से आश्चर्यचकित हैं? अपने अध्यापक और कक्षा के सहयोगियों के साथ उत्तर की सार्थकता पर चर्चा कीजिए।

प्रश्न 5.
![]() के दशमलव प्रसार में अंकों के पुनरावृत्ति खण्ड में अंकों की अधिकतम संख्या क्या हो सकती है? अपने उत्तर की जाँच करने के लिए विभाजन-क्रिया कीजिए।
के दशमलव प्रसार में अंकों के पुनरावृत्ति खण्ड में अंकों की अधिकतम संख्या क्या हो सकती है? अपने उत्तर की जाँच करने के लिए विभाजन-क्रिया कीजिए।
हल:
![]() में हर 17 है। अत: भाग करने पर 1 से 16 तक की कोई भी संख्याएँ शेषफल के रूप में प्राप्त हो सकती है। उसके उपरान्त अंकों की पुनरावृत्ति अवश्य होगी।
में हर 17 है। अत: भाग करने पर 1 से 16 तक की कोई भी संख्याएँ शेषफल के रूप में प्राप्त हो सकती है। उसके उपरान्त अंकों की पुनरावृत्ति अवश्य होगी।
अतः ![]() के दशमलव प्रसार के पुनरावृत्ति खण्ड में अधिकतम अंक = 16
के दशमलव प्रसार के पुनरावृत्ति खण्ड में अधिकतम अंक = 16

प्रश्न 6.
![]() , q ≠ 0 के रूप में परिमेय संख्याओं के अनेक उदाहरण लीजिए, जहाँ p और q पूर्णांक हैं, जिनका 1 के अतिरिक्त अन्य कोई उभयनिष्ठ गुणनखण्ड नहीं है और जिसका सांत दशमलव निरूपण (प्रसार) है। क्या आप यह अनुमान लगा सकते हैं कि q को कौन-सा गुण अवश्य सन्तुष्ट करना चाहिए?
, q ≠ 0 के रूप में परिमेय संख्याओं के अनेक उदाहरण लीजिए, जहाँ p और q पूर्णांक हैं, जिनका 1 के अतिरिक्त अन्य कोई उभयनिष्ठ गुणनखण्ड नहीं है और जिसका सांत दशमलव निरूपण (प्रसार) है। क्या आप यह अनुमान लगा सकते हैं कि q को कौन-सा गुण अवश्य सन्तुष्ट करना चाहिए?
हल :
![]() के रूप में परिमेय संख्याओं का दशमलव प्रसार सांत तभी होगा जब p को qसे भाग देने पर शेषफल शून्य हो। जबकि p और g में 1 के अतिरिक्त कोई उभयनिष्ठ गुणनखण्ड न हो जहाँ p और q पूर्णांक हैं तथा q ≠ 0 है।
के रूप में परिमेय संख्याओं का दशमलव प्रसार सांत तभी होगा जब p को qसे भाग देने पर शेषफल शून्य हो। जबकि p और g में 1 के अतिरिक्त कोई उभयनिष्ठ गुणनखण्ड न हो जहाँ p और q पूर्णांक हैं तथा q ≠ 0 है।
किसी संख्या को भाग करने पर शेषफल शून्य तभी होगा जबकि
(1) भाजक 2 या 2 की कोई घात हो।
(2) भाजक 5 या 6 की कोई घात हो।
(3) भाजक 2 की किसी घात और 5 की किसी घात का गुणनफल हो।
अतः q को 2 अथवा 5 अथवा इनकी किसी घात के बराबर होना चाहिए अथवा 2 की किसी घात और 5 की किसी घात के गुणन के बराबर होना चाहिए।
अर्थात q = 2m x 5n जहाँ m और n पूर्ण संख्याएँ हैं।
प्रश्न 7.
ऐसी तीन संख्याएँ लिखिए जिनके दशमलव प्रसार अनवसानी अनावर्ती हो।
हल :
सभी अपरिमेय संख्याओं के दशमलव प्रसार अनवसानी अनावर्ती होते हैं।
ऐसी तीन संख्याएँ √2, √3, √5 हैं।
प्रश्न 8.
परिमेय संख्याओं और
के बीच की तीन अलग-अलग अपरिमेय संख्याएँ ज्ञात कीजिए।

प्रश्न 9.
बताइए कि निम्नलिखित संख्याओं में कौन-कौन सी संख्याएँ परिमेय और कौन-कौन भी संख्याएँ अपरिमेय हैं :

प्रश्नावली 1.4
प्रश्न 1.
उत्तरोत्तर आवर्धन करके संख्या-रेखा पर 3.765 को देखिए।
हल :
चरण 1 : दी गई संख्या 3 तथा 4 के मध्य स्थित है।
चरण 2 : 3 और 4 के मध्य अन्तराल का आवर्धन करते हैं तथा इसे 10 बराबर भागों में विभाजित करते हैं।
चरण 3 : दी गई संख्या 3.7 और 3.8 के मध्य स्थित हैं।
चरण 4 : 3.7 और 3.8 के मध्य अन्तराल को 10 बराबर भागों में विभाजित करते हैं तथा इसका आवर्धन करते हैं।
चरण 5 : दी गई संख्या 3.76 तथा 3.77 के मध्य स्थित हैं।
चरण 6 : 3.76 और 3.77 के मध्य अन्तराल का आवर्धन करते हैं तथा इसे 10 बराबर भागों में विभाजित करते हैं।
चरण 7 : चरण-6 के आवर्धन में 3.765 पाँचवाँ भाग हैं।

प्रश्न 2.
4 दशमलव स्थानों तक संख्या-रेखा पर 4.26 को देखिए।
हल :
चरण 1 : संख्या रेखा पर दी गई संख्या 4.26, 4 तथा 5 के मध्य स्थित हैं। (4 दशमलव स्थानों तक संख्या 4.2626 हैं।)
चरण 2 : 4 तथा 5 के मध्य अन्तराल का आवर्धन करते हैं और इसे 10 बराबर भागों में विभाजित करते हैं।
चरण 3 : दी गई संख्या 4.2626, 4.2 तथा 4.3 के मध्य स्थित हैं।
चरण 4 : 4.2 तथा 4.3 के मध्य अन्तराल का आवर्धन करते हैं और इसे 10 बराबर भागों में विभाजित करते हैं।
चरण 5 : दी गई संख्या 4.26 और 4.27 के मध्य स्थित हैं।
चरण 6 : 4.26 तथा 4.27 के मध्य अन्तराल का आवर्धन करते हैं और इसे 10 बराबर भागों में विभाजित करते हैं।
चरण 7 : दी गई संख्या 4.262 तथा 4.263 के मध्य स्थित हैं।
चरण 8 : 4.262 तथा 4.263 के मध्य अन्तराल का आवर्धन करते हैं और इसे 10 बराबर भागों में विभाजित करते हैं।
चरण 9 : चरण-8 के आवर्धन में 4.2626 छठवाँ भाग हैं।

प्रश्नावली 1.5
प्रश्न 1.
बताइए नीचे दी गयी संख्याओं में कौन-कौन परिमेय हैं और कौन-कौन अपरिमेय हैं :


प्रश्न 2.
निम्नलिखित व्यंजकों में से प्रत्येक व्यंजक को सरल कीजिए।

प्रश्न 3.
आपको याद होगा कि π को एक वृत्त की परिधि (c) और उसके व्यास (d) के अनुपात से परिभाषित किया जाता है अर्थात् π = है। यह इस तथ्य का अन्तर्विरोध करता हुआ प्रतीत होता है कि π अपरिमेय है। इस अन्तर्विरोध का निराकरण आप किस प्रकार करेंगे?

c और d को किसी पैमाने से मापने पर हमें केवल सन्निकट माप प्राप्त होती है जिससे यह पता नहीं चल पाती कि c या d परिमेय संख्याएँ हैं या अपरिमेय संख्याएँ हैं। इसी कारण हमें c और d को परिमेय संख्याएँ समझने का भ्रम उत्पन्न होता है। और हम c और d के अनुपात 7 को परिमेय संख्या समझने की ओर अग्रसर होते है जिससे अन्तर्विरोध उत्पन्न होता है। वास्तव में 7 के अपरिमेय होने में कोई अन्तर्विरोध नहीं है।
प्रश्न 4.
संख्या रेखा पर √9.3 को निरूपित कीजिए।
हल :
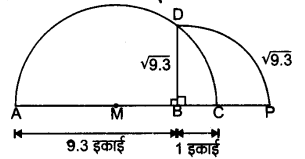
रेखाखण्ड AB = 9.3 मात्रक और BC = 1 मात्रक इस प्रकार खींचते हैं कि ABC एक सरल रेखा है।
AC का मध्य-बिन्दु M ज्ञात करते हैं तथा AC को व्यास लेकर अर्द्धवृत्त खींचते हैं।
∠ABD = 90° बनाते हैं जो अर्द्धवृत्त को D पर काटता है।
अब संख्या रेखा पर B को केन्द्र लेकर BD त्रिज्या से चाप लगाते हैं जो संख्या रेखा को P पर काटता है।
अब √9.3 = BP अर्थात् बिन्दु P संख्या रेखा पर √9.3 को निरूपित करती है।
प्रश्न 5.
निम्नलिखित के हरों का परिमेयकरण कीजिए ।



प्रश्नावली 1.6
प्रश्न 1.
ज्ञात कीजिए :

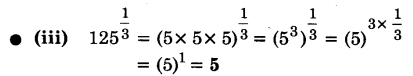
प्रश्न 2.
ज्ञात कीजिए।
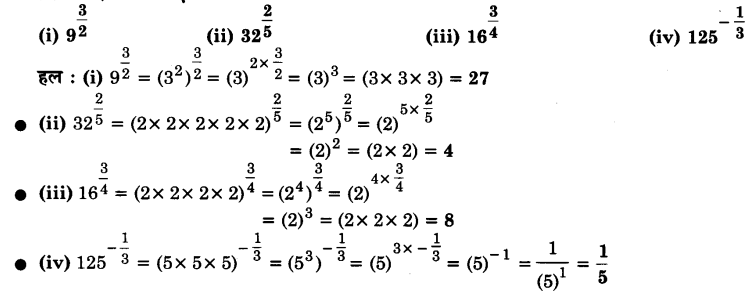
प्रश्न 3.
सरल कीजिए :
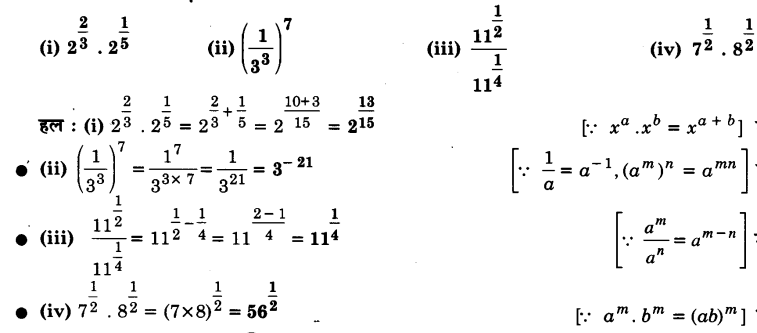
We hope the UP Board Solutions for Class 9 Maths Chapter 1 Number systems (संख्या पद्धति) help you.
5 Responses
very nice
My name is vivek yadav
Class 9
Student
3/4 ke madya 6 parmey sankhya
Tihtfhjeg
Hhff
Ghkjh
Vbjkkn
Bnjg
Hjjhf
Bbjgddf
Hhgf4ghj
Hii
Ashraf husain