UP Board Solutions for Class 9 Maths Chapter 6 Lines and Angles (रेखाएँ और कोण)
These Solutions are part of UP Board Solutions for Class 9 Maths. Here we have given UP Board Solutions for Class 9 Maths Chapter 6 Lines and Angles (रेखाएँ और कोण).
प्रश्नावलीं 6.1
प्रश्न 1.
दी गई आकृति में रेखाएँ AB और CD बिन्दु O पर प्रतिच्छेद करती हैं। यदि ∠AOC + ∠BOE = 70° है और ∠BOD = 40° है तो ∠BOE और प्रतिवर्ती ∠COE ज्ञात कीजिए।
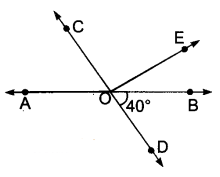
हल :
रेखाएँ AB तथा CD बिन्दु O पर प्रतिच्छेद करती हैं।
∠AOC = ∠BOD (शीर्षाभिमुख कोण)
दिया है :
∠BOD = 40°
∠AOC = 40° …(1)
यह भी ज्ञात है कि ∠AOC + ∠BOE = 70°
∠BOE = 70° – ∠AOC
∠BOE = 70° – 40°
∠BOE = 30°
AB एक ऋजु रेखा है और उस पर स्थित बिन्दु O से OC तथा OE मिलती हैं।
∠AOC + ∠COE + ∠BOE = 180°
40° + ∠COE + 30° = 180°
∠COE = 180° – 40° – 30°
∠COE = 110°
तब प्रतिवर्ती ∠COE = 360° – 110° = 250°
अतः ∠BOE = 30° तथा प्रतिवर्ती ∠COE = 250°
प्रश्न 2.
दी गई आकृति में रेखाएँ XY और MN बिन्दु0 पर प्रतिच्छेद करती हैं। यदि ∠POY = 90° और d : b = 2 : 3 हो तो c ज्ञात कीजिए।

हल :
XY एक ऋजु रेखा है और ∠POY = 90°
∠POX + ∠POY = 180° (रेखीय युग्म)
परन्तु ∠POY = 90°
घटाने पर, ∠POX = 90°
∠POM + ∠MOX = a + b = 90° …(1)
दिया है :
a : b = 2 : 3
⇒ ![]() =
= ![]()
⇒ 2b = 3a
⇒ b = ![]() a
a
समीकरण (1) से,
a + b = 90°
⇒ a + ![]() a = 90° (b =
a = 90° (b = ![]() a)
a)
⇒ ![]() = 90°
= 90°
⇒ 5a = 180°
⇒ a = 36° ……(2)
ऋजु रेखाएँ XY और MN बिन्दु O पर प्रतिच्छेद करती हैं।
∠XON = ∠YOM (शीर्षाभिमुख कोण)
∠XON = ∠MOP + ∠POY (आकृति से)
c = 2 + 90°
c = 36° + 90° = 126°
अतः c = 126°
प्रश्न 3.
दी गई आकृति में, यदि ∠PQR = ∠PRQ है तो सिद्ध कीजिए कि ∠PQS = ∠PRT है।

हल :
दी गई आकृति में SR एक ऋजु रेखा है और उसके बिन्दु Q पर रेखा PQ मिलती है।
∠PQS तथा ∠PQR एक रैखिक युग्म के कोण हैं।
∠PQS + ∠PQR = 180° …..(1)
पुनः QT एक ऋजु रेखा है जिसके बिन्दु R पर रेखा PR मिलती है।
अतः ∠PRT और ∠PRQ भी एक रैखिक युग्म के कोण हैं।
∠PRQ + ∠PRT = 180° ………(2)
समीकरण (1) व समीकरण (2) से,
∠PQS + ∠PQR = ∠PRQ + ∠PRT ……(3)
परन्तु दिया है कि ∠PQR = ∠PRQ ………(4)
तब समीकरण (3) में से समीकरण (4) को घटाने पर,
∠PQS = ∠PRT
Proved.
प्रश्न 4.
दी गई आकृति में यदि x + y = w + z है तो सिद्ध कीजिए कि AOB एक ऋजु रेखा है।
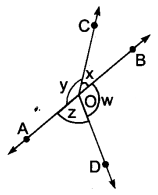
हल :
∠x, ∠y, ∠w व ∠z एक ही बिन्दु O पर बने हैं।
x + y + w + z = 360° …….(1)
परन्तु दिया है कि x + y = w + z
x + y – w – z = 0 ……..(2)
समीकरण (1) व समीकरण (2) को जोड़ने पर,
2x + 2y = 360°
⇒ x + y = 180° …(3)
समीकरण (3) से ∠x व ∠y दो आसन्न कोण हैं जिनका योग 180° है तथा रेखा OC दोनों कोणों की उभयनिष्ठ रेखा है, तब इन कोणों की शेष भुजाएँ AO तथा OB एक सरल रेखा बनाएँगी।
अत: AOB एक ऋजु रेखा है।
Proved.
प्रश्न 5.
दी गई आकृति में, POQ एक रेखा है। किरण OR रेखा PQ पर लम्ब है। किरणों OP और OR के बीच में Os एक अन्य किरण है। सिद्ध कीजिए :
∠ROS = ![]() (∠QOS – ∠POS)
(∠QOS – ∠POS)

हल :
POQ एक ऋजु रेखा है और किरण OR, रेखा PQ पर लम्ब है।
∠QOR = 90° और ∠POR = 90°
∠POR = 90°
∠POS + ∠ROS = 90° (आकृति से)
∠POS = 90° – ∠ROS …(1)
∠QOS = ∠ROS + ∠QOR (आकृति से)
∠QOS = ∠ROS + 90° …..(2)
समीकरण (2) में से समीकरण (1) को घटाने पर,
∠QOS – ∠POS = (∠ROS + 90°) – (90° – ∠ROS)
∠QOS – ∠POS = ∠ROS + 90° – 90° + ∠ROS
(∠QOS – ∠POS) = 2 ∠ROS
![]() (∠QOS – ∠POS) = ∠ROS
(∠QOS – ∠POS) = ∠ROS
अतः ∠ROS = ![]() (∠QOS – ∠POS)
(∠QOS – ∠POS)
Proved.
प्रश्न 6.
यह दिया है कि ∠XYZ = 64° है और XY को बिन्दु P तक बढ़ाया गया है। दी। हुई सूचना से एक आकृति खींचिए। यदि किरण YQ, ∠ZYP को समद्विभाजित करती है तो ∠XYQ और प्रतिवर्ती ∠QYP के मान ज्ञात कीजिए।

हल :
दी गई सूचना से आकृति खींचना :
(i) एक किरण YZ खींची।
(ii) किरण YZ के बिन्दु Y पर ∠XYZ = 64° खींचा।
(iii) XY को बिन्दु P तक बढ़ाकर रेखा XYP खींची।
तत्पश्चात् दूसरी आकृति बनाकर बिन्दु Y से किरण YQ इस प्रकार खींची कि किरण YQ, ∠ZYP को समद्विभाजित करे।
निर्दिष्ट कोणों की माप की गणना :

(i) ∠XYQ
∠XYZ की कोण-रेखा XY को बिन्दु P तक बढ़ाया गया है।
XYP एक ऋजु रेखा है।
तब, ∠XYZ और ∠ZYP कोणों का युग्म एक रैखिक युग्म है।
∠XYZ + ∠ZYP = 180°
64° + ∠ZYP = 180° (दिया है ∠XYZ = 64°)
∠ZYP = 180° – 64° = 116°
किरण YQ, ∠ZYP को समद्विभाजित करती है।
∠ZYQ = ∠QYP और ∠ZYQ + ∠QYP = 116°
हल करने पर, ∠ZYQ = 58° और ∠QYP = 58° …(1)
अब चूँकि ∠XYQ = ∠XYZ + ∠ZYQ (आकृति से)
= 64° + 58° = 122°
अतः ∠XYQ = 122°
(ii) प्रतिवर्ती ∠QYP समीकरण (1) से,
∠QYP = 58° प्रतिवर्ती ∠QYP = 360° – 58° = 302°
अत: प्रतिवर्ती ∠QYP = 302°
प्रश्नावली 6.2
प्रश्न 1.
दी गई आकृति में, और y के मान ज्ञात कीजिए और फिर दर्शाइए कि AB || CD है।

हल :
दी गई आकृति में ऋजु रेखा AB पर एक तिर्यक (तिरछी) रेखा 50° के कोण पर झुकी है। तब, यह 50° का कोण और ∠x एक रैखिक (कोण) युग्म बनाते हैं।
50° + ∠x = 180°
∠x = 180° – 50° = 130°
पुनः ऋजु रेखा CD को एक अन्य तिर्यक ऋजु रेखा काटती है।
∠y और चित्र में बना 130° के कोण शीर्षाभिमुख कोण युग्म के कोण हैं जिससे
∠y = 130°
∠x और ∠y एकान्तर अन्त:कोण हैं और परस्पर बराबर भी हैं।
यह समान्तर रेखाओं को तिर्यक रेखा के काटने से बनेंगे
अत: ऋजु रेखा AB || CD
प्रश्न 2.
दी गई आकृति में, यदि AB || CD; CD || EF और y : 2 = 3: 7 है। तो x का मान ज्ञात कीजिए।

हल :
दी गई आकृति में AB || CD और CD || EF
AB || EF
अब चूँकि AB || EF को एक तिर्यक ऋजु रेखा l काटती है जिससे एकान्तर कोण ∠x और ∠y बनते हैं।
∠x = ∠y ……(1)
AB || CD और एक तिर्यक रेखा l इन्हें काटती है जिससे ∠x और ∠y, तिर्यक रेखा l के एक ही ओर बने अन्त:कोण हैं।
∠x + ∠y = 180° …(2)
तब समीकरण (1) व समीकरण (2) से,
∠y + ∠z = 180° ……..(3)
y : 2 = 3 : 7 तब माना y = 3k तथा z = 7k
y और z के ये मान समीकरण (3) में रखने पर,
3k + 7k = 180°
⇒ 10k = 180°
⇒ k = 18°
z = 7k = 7 x 18° = 126°
समीकरण (1) से,
∠x = ∠z और z = 126° .
∠x = 126°
अतः x = 126°
प्रश्न 3.
दी गई आकृति में, यदि AB || CD, EF ⊥ CD और ∠GED = 126° हो तो ∠AGE, ∠GEF और ∠FGE ज्ञात कीजिए।

हल :
AB || CD और GE एक तिर्यक रेखा है।
∠AGE = ∠GED (एकान्तर कोण)
⇒ ∠AGE = 126° (∠GED = 126°)
⇒ ∠GED = 126°
⇒ ∠GEF + ∠FED = 126°
⇒ ∠GEF + 90° = 126° (∠ZFED = 90°)
⇒ ∠GEF = 126° – 90° = 36°
⇒ ∠GEF = 36°
पुनः AB एक ऋजु रेखा है और GE, उससे बिन्दु G पर मिलती है।
∠AGE और ∠FGE एक रैखिक कोण-युग्म बनाते हैं।
∠AGE + ∠FGE = 180°
⇒ 126° + ∠FGE = 180° (∠AGE = 126° अभी ऊपर ज्ञात किया है।)
⇒ ∠FGE = 180° – 126°
⇒ ∠FGE = 54°
अतः ∠AGE = 126°, ∠GEF = 36° और ∠FGE = 54°
प्रश्न 4.
दी गई आकृति में, यदि PQ || ST, ∠PQR = 110° और ∠RST = 130° हो तो ∠QRS ज्ञात कीजिए।
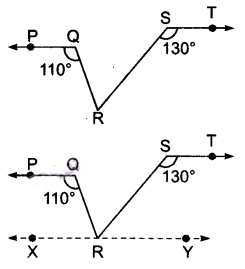
हल :
दिया है : दी गई आकृति में PQ || ST , ∠PQR = 110° तथा ∠RST = 130°
ज्ञात करना है : ∠QRS की माप।
रचना : बिन्दु R से PQ के समान्तर एक ऋजु रेखा XY खींची।
विश्लेषण : PQ || XY (रचना से) और QR तिर्यक रेखा है जो इन्हें Q तथा R पर काटती है।
∠PQR और ∠QRX, QR के एक ही ओर बने अन्त: कोण हैं।
∠PQR + ∠QRX = 180°
⇒ ∠QRX = 180° – ∠PQR = 180° – 110° (ZPQR = 110°)
⇒ ∠QRX = 70°
अब :: PQ || XY रचना से और PQ || ST दिया है।
ST || XY
ST || XY और RS तिर्यक रेखा है।
∠SRY और ∠RST तिर्यक रेखा के एक ही ओर बने अन्त: कोण हैं।
∠SRY + ∠RST = 180°
⇒ ∠SRY + 130° = 180° (∠RST = 130°)
⇒ ∠SRY = 180° – 130°
⇒ ∠SRY = 50°
पुनः ∠QRX, ∠QRS और ∠SRY एक ही ऋजु रेखा के बिन्दु R पर रेखा XY के एक ही ओर बने हैं।
∠QRX + ∠QRS + ∠SRY = 180° (आकृति से)
⇒ 70° + ∠QRS + 50° = 180°
⇒ ∠QRS = 180° – 70° – 50° = 60°
अतः ∠QRS = 60°
प्रश्न 5.
दी गई आकृति में, यदि AB || CD, ∠APQ = 50° और ∠PRD = 127° है तो x और y ज्ञात कीजिए।
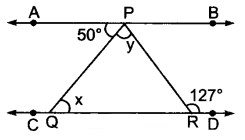
हल :
दिया है : ऋजु रेखा AB || CD, ∠APQ = 50° और ∠PRD = 127°
ज्ञात करना है : x तथा y
विश्लेषण : AB|| CD और PQ एक तिर्यक रेखा है।
∠APQ = ∠PQR (एकान्तर कोण युग्म)
50° = x
x = 50°
पुनः AB || CD और PR एक तिर्यक रेखा है।
∠APR = ∠PRD (एकान्तर कोण युग्म)
∠APQ + ∠QPR = ∠PRD (∠APR = ∠APQ + ∠QPR, चित्र से)
50° + y = 127°
y = 127° – 50° = 77°
अतः x = 50° और y = 77°
प्रश्न 6.
दी गई आकृति में P और RS दो दर्पण हैं जो एक-दूसरे के समान्तर रखे गए हैं। एक आपतन किरण (Incident Ray) AB, दर्पण PQ से B पर टकराती है और परावर्तित किरण (Reflected Ray) पथ BC पर चलकर दर्पण RS से C पर टकराती है तथा पुनः CD के अनुदिश परावर्तित हो जाती है। सिद्ध कीजिए कि AB || CD है।

हल :
दिया है : दर्पण PQ || दर्पण RS तथा AB और BC दर्पण PQ के लिए क्रमश: आपतित और परावर्तित किरणें हैं। दर्पण RS के लिए आपतित किरण BC तथा परावर्तित किरण CD है।
BP’ दर्पण PQ के बिन्दु B पर तथा CQ’ दर्पण RS के बिन्दु C पर अभिलम्ब हैं।
सिद्ध करना है : AB || CD
उपपत्ति : BP’, बिन्दु B पर अभिलम्ब है;
अतः BP’ ⊥ PQ
और CQ’, बिन्दु C पर अभिलम्ब है;
अतः CQ ⊥ RS
PQ || RS
उक्त तीनों तथ्यों से BP’ || CQ’ और BC तिर्यक रेखा है।
∠P’BC = ∠Q’CB (एकान्तर कोण)
∠r1 = ∠i2 …..(1)
परावर्तन के नियमों से,
∠i1 = ∠r1 …..(2)
∠i2 = ∠r2 ……(3)
समीकरण (1), (2) व (3) से,
∠i1 = ∠r2
समीकरण (1) व समीकरण (4) को जोड़ने पर,
∠(i1 + r1) = ∠(i2 + r2)
∠ABC = ∠BCD
परन्तु ये AB तथा CD को BC द्वारा प्रतिच्छेद करने से निर्मित समान एकान्तर कोण हैं।
अत: AB || CD
Proved.
प्रश्नावली 6.3
प्रश्न 1.
दी गई आकृति में ΔPQR की भुजाओं QP और RQ को क्रमशः बिन्दुओं S और T तक बढ़ाया गया है। यदि ∠SPR = 135° है और ∠PQT = 110° है तो ∠PRQ ज्ञात कीजिए।

हल :
ΔPQR की भुजा QP को बिन्दु S तक बढ़ाया गया है जिससे
बहिष्कोण ∠SPR = ∠PQR + ∠PRQ . (किसी त्रिभुज का एक बहिष्कोण उसके अन्तः अभिमुख कोणों के योगफल के बराबर होता है।)
परन्तु दिया है :
∠SPR = 135°
∠SPR = 135°
∠PQR + ∠PRQ = 135° …….(1)
पुनः ΔPQR की भुजा RQ को बिन्दु T तक बढ़ाया गया है जिससे
बहिष्कोण ∠PQT = ∠QPR + ∠PRQ
(किसी त्रिभुज का एक बहिष्कोण उसके अन्तः अभिमुख कोणों के योगफल के बराबर होता है।)
परन्तु ज्ञात है कि
∠PQT = 110°
∠QPR + ∠PRQ = 110° …….(2)
समीकरण (1) व समीकरण (2) को जोड़ने पर,
∠PQR + ∠QPR + ∠PRQ + ∠PRQ = 245° …(3)
परन्तु ΔPQR में,
∠PQR + ∠QPR +∠PRQ = 180° (त्रिभुज के अन्त:कोणों का योग 180° होता है।)
समीकरण (3) से (4) को घटाने पर,
∠PRQ = 65°
अतः ∠PRQ = 65°
प्रश्न 2.
दी गई आकृति में, ∠X = 62° और ∠XYZ = 54° है। यदि YO और ZO क्रमशः ΔXYZ के ∠XYZ और ∠XZY के समद्विभाजक हैं तो ∠OZY और ∠YOZ ज्ञात कीजिए।

हल :
ΔXYZ में,
∠X + ∠XYZ + ∠XZY = 180° ( त्रिभुज के अन्त:कोणों का योग 180° होता है)
62° + 54° + ∠XZY = 180°
⇒ ∠XZY = 180° – (62° + 54°) = 180° – 116°
⇒ ∠XZY = 64°
YO, ∠XYZ का और ZO, ∠XZY का समद्विभाजक है।
∠OYZ = ![]() ∠XYZ और ∠OZY =
∠XYZ और ∠OZY = ![]() ∠XZY
∠XZY
⇒ ∠OYZ = ![]() x 54° और ∠OZY =
x 54° और ∠OZY = ![]() x 64°
x 64°
⇒ ∠OYZ = 27° और ∠OZY = 32°
तब, ΔOYZ में, ∠OYZ + ∠OZY + ∠YOZ = 180°
(त्रिभुज के अन्त:कोणों का योग 180° होता है।)
27° + 32° + ∠YOZ = 180°
⇒ ∠YOZ = 180° – (27° + 32°) = 180° – 59°
⇒ ∠YOZ = 121°
अतः ∠OZY = 32°
तथा ∠YOZ = 121°
प्रश्न 3.
दी गई आकृति में, यदि AB || DE, ∠BAC = 35° और ∠CDE = 53° है तो ∠DCE ज्ञात कीजिए।

हल :
AB || DE और ऋजु रेखा AE इन्हें काटती है।
तब, ∠BAE = ∠AED (एकान्तर कोण)
परन्तु ∠BAE = ∠BAC और ∠AED = ∠CED
∠BAC = ∠CED
⇒ 35° = ∠CED
⇒ ∠CED = 35°
तब, ΔCDE में,
∠CDE + ∠CED + ∠DCE = 180° (त्रिभुज के अन्त:कोणों का योग 180° होता है।)
⇒ 53° + 35° + ∠DCE = 180°
⇒ ∠DCE = 180° – (53° + 35°) = 180° – 88° = 92°
अतः ∠DCE = 92°
प्रश्न 4.
दी गई आकृति में यदि रेखाएँ PQ और RS बिन्दु T पर इस प्रकार प्रतिच्छेद करती हैं कि ∠PRT = 40°, ∠RPT = 95° और ∠TSQ = 75° है तो ∠SQT ज्ञात कीजिए।

हल :
ΔPRT में,
∠PRT + ∠RPT + ∠PTR = 180° (त्रिभुज के अन्त:कोणों का योग 180° होता है।)
⇒ 40° + 95° + ∠PTR = 180°
⇒ ∠PTR = 180° – (95° + 40°) = 180° – 135°
⇒ ∠PTR = 45°
ऋजु रेखाएँ PQ और RS परस्पर बिन्दु T पर प्रतिच्छेद करती हैं।
∠QTS = ∠PTR (शीर्षाभिमुख कोण)
∠QTS = 45°
∠PTR = 45°
अब, ΔQTS में, ∠QTS + ∠TSQ + ∠SQT = 180°
(त्रिभुज के अन्त:कोणों का योग 180° होता है।)
45° + 75° + ∠SQT = 180°
⇒ ∠SQT = 180° – (45° + 75°) = 180° – 120° = 60°
अतः
∠SQT = 60°
प्रश्न 5.
दी गई आकृति में, यदि PQ ⊥ PS, PQ || SR, ∠SQR = 28° और ∠QRT = 65° है तो x और y का मान ज्ञात कीजिए।

हल :
ΔQRS में ∠QRT बहिष्कोण है।
∠SQR + ∠QSR = ∠QRT (किसी त्रिभुज का एक बहिष्कोण उसके अन्तः अभिमुख कोणों के योगफल के बराबर होता है।)
28° + ∠QSR = 65°
⇒ ∠QSR = 65° – 28° = 37°
अब, PQ || SR और QS एक तिर्यक प्रतिच्छेदी रेखा है,
∠PQS = ∠QSR (एकान्तर कोण)
x = 37°
PQ ⊥ PS
∠P = 90°
ΔPQS में ∠P + ∠PQS + ∠PSQ = 180° (त्रिभुज के अन्त: कोणों का योग 180° होता है।)
90° + x + y = 180°
⇒ x + y = 90°
⇒ 37° + y = 90°
⇒ y = 90° – 37° = 53°
x = 37° तथा y = 53°
प्रश्न 6.
दी गई आकृति में ΔPQR की भुजा QR को बिन्दु S तक बढ़ाया P गया है। यदि ∠PQR और ∠PRS के समद्विभाजक बिन्दु T पर मिलते हैं तो सिद्ध कीजिए कि ∠QTR = ![]() ∠QPR
∠QPR

हल :
ΔPQR में,
∠PQR + ∠PRQ + ∠QPR = 180°
तथा ΔTQR में,
∠TQR + ∠QRT + ∠QTR = 180° (त्रिभुज के अन्त:कोणों का योग 180° होता है।)
∠TQR + ∠QRT + ∠QTR = ∠PQR + ∠PRQ + ∠QPR
∠TQR + (∠PRQ + ∠PRT) + ∠QTR = ∠PQR + ∠PRQ + ∠QPR [∴ ∠QRT = ∠PRQ + ∠PRT]
∠TQR + ∠PRQ + ∠PRT + ∠QTR = ∠PQR + ∠PRQ + ∠QPR
∠TQR + ∠PRT + ∠QTR = ∠PQR + ∠QPR …….(1)
QT, ∠PQR का समद्विभाजक है।
∠TQR = ![]() ∠PQR ⇒ ∠PQR = 2 ∠TQR ……..(2)
∠PQR ⇒ ∠PQR = 2 ∠TQR ……..(2)
समीकरण (1) वे समीकरण (2) से,
∠TQR + ∠PRT + ∠QTR = 2 ∠TQR + ∠QPR
∠PRT + ∠QTR = ∠TQR + ∠QPR
RT, ∠PRS का समद्विभाजक है।
∠PRT = ![]() ∠PRS
∠PRS
और ∠PRS, ΔPQR का बहिष्कोण है।
∠PRS = ∠PQR + ∠QPR (किसी त्रिभुज का एक बहिष्कोण उसके अन्तः अभिमुख कोणों के योगफल के बराबर होता है।)
∠PRS = 2 ∠TQR + ∠QPR [समीकरण (2) से] …(4)
∠PRT = ![]() ∠PRS =
∠PRS = ![]() (2 ∠TQR + ∠QPR) [समीकरण (4) से
(2 ∠TQR + ∠QPR) [समीकरण (4) से
∠PRT = ∠TQR + ![]() ∠QPR …(5)
∠QPR …(5)
समीकरण (3) में से समीकरण (5) को घटाने पर,
∠QTR = ∠QPR – ![]() ∠QPR
∠QPR
∠QTR = ![]() ∠QPR
∠QPR
Proved.
We hope the UP Board Solutions for Class 9 Maths Chapter 6 Lines and Angles (रेखाएँ और कोण) help you.
One Response
Maths answer