UP Board Solutions for Class 9 Maths Chapter 12 Heron’s Formula (हीरोन सूत्र)
These Solutions are part of UP Board Solutions for Class 9 Maths. Here we have given UP Board Solutions for Class 9 Maths Chapter 12 Heron’s Formula (हीरोन सूत्र).
प्रश्नावली 12.1
प्रश्न 1. एक यातायात संकेत बोर्ड पर ‘आगे स्कूल है’ लिखा है और यह भुजा ‘a’ वाले एक समबाहु त्रिभुज के आकार का है। हीरोन के सूत्र का प्रयोग करके इस बोर्ड का क्षेत्रफल ज्ञात कीजिए। यदि संकेत बोर्ड पर परिमाप 180 सेमी है तो इसका क्षेत्रफल क्या होगा?
हल :
दिया है, समबाहु त्रिभुज के आकार के बोर्ड की एक भुजा = a
समबाहु त्रिभुज के आकार के बोर्ड का परिमाप = a + a + a = 3a
त्रिभुज का अर्द्धपरिमाप s =

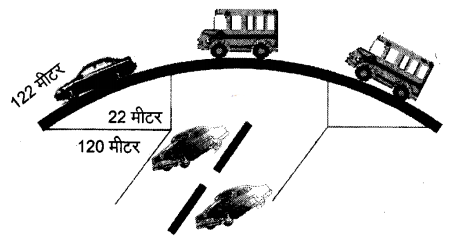
प्रश्न 2. किसी फ्लाईओवर (flyover) की त्रिभुजाकार दीवार को विज्ञापनों के लिए प्रयोग किया जाता है। दीवार की भुजाओं की लम्बाइयाँ 122 मीटर, 22 मीटर और 120 मीटर हैं। इस विज्ञापन से प्रतिवर्ष 5000 प्रति मीटर² की प्राप्ति होती है। एक कम्पनी ने एक दीवार को विज्ञापन देने के लिए 3 महीने के लिए किराए पर लिया। उसने कुल कितना किराया दिया?
हल :
फ्लाईओवर की त्रिभुजाकार दीवार की मापें 122 मीटर, 22 मीटर तथा 120 मीटर हैं।
माना a = 122 मीटर, b = 22 मीटर, c = 120 मीटर

प्रश्न 3. किसी पार्क में एक फिसल (slide) पट्टी बनी हुई है। इसकी पाश्र्वीय दीवारों (slide walls) में से एक दीवार पर किसी रंग से पेन्ट किया गया है और उस पर “पार्क को हरा-भरा और साफ रखिए’ लिखा हुआ है। यदि इस दीवार की विमाएँ 15 मीटर, 11 मीटर और 6 मीटर हैं तो रंग से पेन्ट हुए भाग
पार्क को हरा-भरा को क्षेत्रफल ज्ञात कीजिए।

हल :
जिस दीवार पर पेन्ट किया गया है, उसकी विमाएँ माना
15 मीटर a = 15 मीटर, b = 11 मीटर और c = 6 मीटर
आकृति में दीवार त्रिभुजाकार है।

प्रश्न 4. उस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसकी दो भुजाएँ 18 सेमी और 10 सेमी हैं तथा परिमाप 42 सेमी है।
हल :
माना त्रिभुजे की दो भुजाएँ a = 18 सेमी तथा b = 10 सेमी
माना तीसरी भुजा c सेमी है।
तब, त्रिभुज की परिमाप = a + b + c = 18 + 10 + c = 28 + c
परन्तु दिया है कि त्रिभुज का परिमाप 42 सेमी है।
28 + c = 42 ⇒ c = 42 – 28 = 14 सेमी

प्रश्न 5. एक त्रिभुज की भुजाओं का अनुपात 12 : 17 : 25 है और उसका परिमाप 640 सेमी है। त्रिभुज का क्षेत्रफले ज्ञात कीजिए।
हल :
दिया है, त्रिभुज की भुजाओं का अनुपात 12 : 17 : 25 है।
माना त्रिभुज की भुजाएँ a = 12 x, b = 17 x तथा c = 25 x
त्रिभुज की परिमाप = a + b + c = 12x + 17x + 25x = 54x
तब, प्रश्नानुसार, त्रिभुज का परिमाप = 540 सेमी

प्रश्न 6. एक समद्विबाहु त्रिभुज का परिमाप 30 सेमी है और उसकी बराबंर भुजाएँ 12 सेमी लम्बी हैं। इस त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
हल :
माना त्रिभुज की तीसरी भुजा c सेमी है।
समद्विबाहु त्रिभुज की बराबर भुजाएँ a = 12 सेमी तथा b = 12 सेमी।
त्रिभुज की परिमाप = a + b + c = 12 + 12 + c = (24 + c) सेमी
परन्तु प्रश्नानुसार, परिमाप 30 सेमी है।
24 + c = 30 ⇒ c = 30 – 24 = 6 सेमी

प्रश्नावली 12.2
प्रश्न 1. एक पार्क चतुर्भुज ABCD के आकार का है, जिसमें ∠C = 90°, AB = 9 मीटर, BC = 12 मीटर, CD = 5 मीटर और AD = 8 मीटर है। इस पार्क का कितना क्षेत्रफल है?

हल :
पार्क का चित्र संलग्न है।
विकर्ण BD खींचा जिसने चतुर्भुजाकार पार्क ABCD को दो त्रिभुजाकार भागों में विभाजित किया हैं।
पहला समकोण त्रिभुज BCD तथा दूसरा विषमबाहु त्रिभुज ABD समकोण त्रिभुज BCD के आकार वाले भाग का क्षेत्रफल
= ![]() x आधार x ऊँचाई
x आधार x ऊँचाई
= ![]() x BC x CD
x BC x CD
= ![]() x 12 x 5 = 30 वर्ग मीटर
x 12 x 5 = 30 वर्ग मीटर
BD, समकोण त्रिभुज BCD का कर्ण है।
पाइथागोरस प्रमेय से, BD² = BC² + CD² = (12)² + (5)² = 144 + 25 = 169 = (13)²
⇒ BD = (13)²
⇒ BD = 13 मीटर
तब, ΔABD में, माना a = 9 मीटर, b = 8 मीटर व c = 13 मीटर

प्रश्न 2. एक चतुर्भुज ABCD का क्षेत्रफल ज्ञात कीजिए, जिसमें AB = 3सेमी, BC = 4सेमी, CD = 4सेमी, DA = 5 सेमी और AC = 5 सेमी है।
हल :
चतुर्भुज ABCD बनाया। स्पष्ट है कि विकर्ण AC संलग्न चतुर्भुज को ΔABC व ΔACD में विभक्त करता है।

प्रश्न 3. राधा ने एक रंगीन कागज से एक हवाईजहाज का चित्र बनाया जैसा कि आकृति में दिखाया गया है। प्रयोग किए गए कागज का कुल क्षेत्रफल ज्ञात कीजिए।


प्रश्न 4. एक त्रिभुज और एक समान्तर चतुर्भुज का एक ही आधार है और क्षेत्रफल भी एक ही है। यदि त्रिभुज की भुजाएँ 26 सेमी, 28 सेमी और 30 सेमी हैं तथा समान्तर चतुर्भुज 28 सेमी के आधार पर स्थित है तो उसकी संगत ऊँचाई ज्ञात कीजिए।

प्रश्न 5. एक समचतुर्भुजाकार घास के खेत में 18 गायों के चरने के लिए घास है। यदि इस समचतुर्भुज की प्रत्येक भुजा 30 मीटर और बड़ा विकर्ण 48 मीटर है तो प्रत्येक गाय को चरने के लिए इस घास के खेत का कितना क्षेत्रफल प्राप्त होगा?

प्रश्न 6. दो विभिन्न रंगों के कपड़ों के 10 त्रिभुजाकार टुकड़ों को सी कर एक छाता बनाया गया है। प्रत्येक टुकड़े के माप 20 सेमी, 50 सेमी और 50 सेमी हैं। छाते में प्रत्येक रंग का कितना कपड़ा लगा है?
हल :
छाते में 2 रंग हैं और उसे 10 त्रिभुजाकार टुकड़ों से सिला गया है।
प्रत्येक रंग के = 5 टुकड़े होंगे।
प्रत्येक त्रिभुजाकार टुकड़े की माप 20, 50 व 50 सेमी हैं अर्थात प्रत्येक टुकड़ा एक समद्विबाहु त्रिभुज को निरूपित करता है।
माना a = 20 सेमी, b = 50 सेमी तथा c = 50 सेमी

= 1000 x 2.4494 वर्ग सेमी
= 2449.4 वर्ग सेमी
अतः प्रत्येक रंग का 2449.4 वर्ग सेमी कपड़ा लगेगा।
प्रश्न 7. एक पतंग तीन भिन्न-भिन्न शेडों (shades) के कागजों से बनी है। इन्हें आकृति में I, II और III से दर्शाया गया है। पतंग का ऊपरी भाग 32 सेमी विकर्ण का एक वर्ग है और निचला भाग 6 सेमी, 6 सेमी और 8 सेमी भुजाओं का एक समद्विबाहु त्रिभुज है। ज्ञात कीजिए कि प्रत्येक शेड का कितना कागज प्रयुक्त किया गया है।
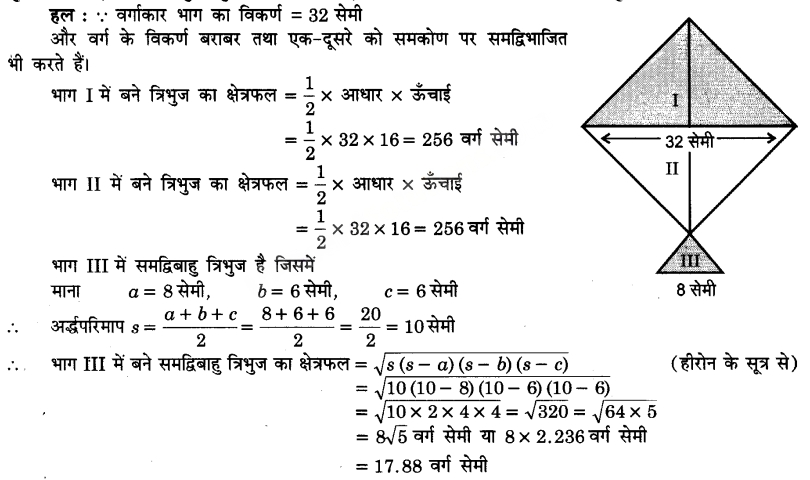
अतः भाग 1 व भाग II प्रत्येक के कागज का क्षेत्रफल= 256 वर्ग सेमी तथा भाग III के लिए कागज का क्षेत्रफल = 17.88 वर्ग सेमी।।
प्रश्न 8. फर्श पर एक फूलों का डिजाइन 16 त्रिभुजाकार टाइलों से बनाया गया है, जिनमें से प्रत्येक की भुजाएँ 9 सेमी, 28 सेमी और 35 सेमी हैं। इन टाइलों को 50 पैसे प्रति सेमी की दर से पॉलिश कराने का व्ययज्ञात कीजिए।

कुल 16 त्रिभुजाकार टाइलों का क्षेत्रफल = 16 x एक त्रिभुजाकार टाइल का क्षेत्रफल
= 16 x 36√6 वर्ग सेमी = 5766 वर्ग सेमी
= 576 x 2.45 = 1411.2 वर्ग सेमी
1 वर्ग सेमी पर पॉलिश कराने का व्यय = 50 पैसे
1411.2 वर्ग सेमी पर पॉलिश कराने का व्यय = 1411.2 x 50 = 70560 पैसे
अतः 16 टाइलों पर पॉलिश कराने का व्यय = 70560 पैसे
प्रश्न 9. एक खेत समलम्ब के आकार का है जिसकी समान्तर भुजाएँ 25 मीटर और 10 मीटर हैं। इसकी असमान्तर भुजाएँ 14 मीटर और 13 मीटर हैं। इस खेत का क्षेत्रफल ज्ञात कीजिए।

