UP Board Solutions for Class 7 Maths Chapter 6 रेखीय समीकरण

UP Board Solutions for Class 7 Maths Chapter 6 रेखीय समीकरण Ex 6(a) are the part of UP Board Solutions for Class 7 Maths. Here we have given UP Board Solutions for Class 7 Maths Chapter 6 रेखीय समीकरण Ex 6(a).

प्रश्न 1.
निम्नलिखित समीकरणों को हल कीजिए एवं अपने उत्तर की जाँच कीजिए

(i) 3x – 5 = 4
हुल:
3x – 5 = 4 =
⇒ 3x = 5 + 4
⇒ 3x = 9
⇒ x = $\frac { 9 }{ 3 }$ =3

उत्तर की जाँचः
बायाँ पक्ष = 3 × 3 – 5 = 9 – 5 = 4
दायाँ पक्ष = 4
अतः बायाँ पक्ष = दायाँ पक्ष

(ii) 5y + 2 = 3y + 8
हल:
5y + 2 = 3y + 8
⇒ 5y – 3y = 8 – 2
⇒ 2y = 6
⇒ y = $\frac { 6 }{ 2 }$ =3

उत्तर की जाँच:
बायाँ पक्ष = 5 × 3 + 2 = 15 + 2 = 17
दायाँ पक्ष = 3 × 3 + 8 = 9 + 8 = 17
अतः बायाँ पक्ष = दायाँ पक्ष।

उत्तर की जाँच : आगे के प्रश्नों में उत्तर की जाँच छात्र उपर्युक्त प्रश्नों की भाँति स्वयं करें।
(iii) 3x + 12 = 24
हल:
3x + 12 = 24
⇒ 3x = 24 – 12
⇒ 3x = 12 =
⇒ x = $\frac { 12 }{ 3 }$ = 4

(iv) 6y – 9 = 2y + 15
हल:
6y – 9 = 2y + 15
⇒ 6y – 2y = 15 + 9
⇒ 4y = 24
⇒ y = $\frac { 24 }{ 4 }$ = 6

(v) 18 – 5y = 3y – 6
हल:
18 – 5y = 3y – 6
⇒ -5y – 3y = 6 – 18
⇒ -8y = -24
⇒ y = $\frac { -24 }{ -8 }$ = 3

प्रश्न 2.
निम्नलिखित समीकरणों को हल कीजिए और उत्तर की जाँच कीजिए

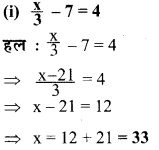
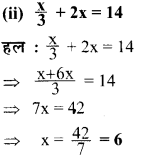
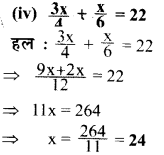
प्रश्न 3.
निम्नलिखित समीकरणों को हल कीजिए और उत्तर की जाँच कीजिए

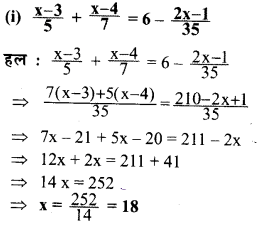
प्रश्न 4.
निम्नलिखित समीकरणों को हल कीजिए?
(i) 1.5y – 7 = 0.5y
हल:
1.5y – 7 = 0.5y
⇒ 1.5y – 0.5y = 7
⇒ y = 7

(ii) 2.8x = 5.4 + x
हल:
2.8x = 5.4 + x
⇒ 2.8x – x = 5.4
⇒ 1.8x = 5.4
⇒ x = $\frac { 5.4 }{ 1.8 }$ = 3

(iii) 0.5y + 0.2y = 0.3y + 2
हल:
0.5y +0.2y = 0.3y + 2
⇒ 5y + 2y –3y = 2
⇒ 4y = 2
⇒ y = $\frac { 2 }{ 4 }$ = 5

(iv) 0.16 (5x – 2) = 0.4x + 7
हल:
0.16 (5x – 2) = 0.4x + 7
⇒ 8x – .32 = 4x + 7
⇒ 8x – 4x 7+ 32
⇒ 4x = 7.32 =
⇒ x = $\frac { 7.32 }{ 4 }$ = 18.3

प्रश्न 5.
निम्नलिखित समीकरणों को हल कीजिए एवं उत्तर की जाँच कीजिए
(i) x + 2(x – 2) + 3x = 35
हल:
x + 2(x – 2) + 3x = 35
⇒ x + 2x – 4 + 3x = 35
⇒ 6x – 4 = 35
⇒ 6x = 39
⇒ x = $\frac { 39 }{ 6 }$ = 6.5

(ii) 3x – 2 (x – 5) = 2 (x + 3) – 8
हल:
3x – 2 (x-5) = 2 (x + 3) – 8
⇒ 3x – 2x + 10 = 2x + 6 – 8
⇒ x – 2x = -2 – 10
⇒ x = – 12
⇒ x = 12

(iii) 15 (y – 4) – 2 (y – 9) + 5 (y + 6) = 0
हल:
15 (y – 4) – 2 (y – 9) + 5 (y + 6) = 0
⇒ 15 y-60 – 2 y + 18 + 5y + 30 = 0
⇒ 15y – 2y + 5y – 60 + 18 + 30 = 0
⇒ 18y – 12 = 0
⇒ 18y = 12
⇒ y = $\frac { 12 }{ 18 } =\frac { 2 }{ 3 }$

(iv) 7 (3 – 2x) +3 (5 – 4x) = 45
हल:
7 (3 – 2x) + 3(5 – 4x) = 45
⇒ 21-14x + 15-12x = 45
⇒ 36 – 26x = 45
⇒ -26x = 45 – 36
⇒ -26x = 9
⇒ x= $-\frac { 9 }{ 26 }$

(v) 3 (15-4x) + 5 (3x – 7) = 15
हल:
3 (15 – 4x) + 5 (3x – 7) = 15
⇒ 45 – 12x + 15x – 35 = 15
⇒ 3x = 15 – 10
⇒ 3x = 5 =
⇒ x = $\frac { 5 }{ 3 }$

अभ्यास 6(b)

प्रश्न 1.
किसी परिमेय संख्या का अंश उसके हर से 3 कम है। यदि उसके अंश और हर में 5 जोड़ दें, तो नई संख्या का मान $\frac { 3 }{ 4 }$ हो जाता है संख्या ज्ञात कीजिए।

प्रश्न 2.
वज्रगुणन विधि से हल कीजिए

प्रश्न 3.
एक भिन्न का हर उसके अंश से 3 अधिक है। यदि अंश और हर दोनों में 5 जोड़ दिया जाता है, तो उसका मान $\frac { 3 }{ 4 }$ ई हो जाता है। भिन्न ज्ञात कीजिए।
हल :
माना किसी संख्या का अंश = x

अभ्यास 6(c)

प्रश्न 1.
सही विकल्प चुनिए
(a) किसी संख्या x और 7 का गुणनफल 28 है, तो वह संख्या है

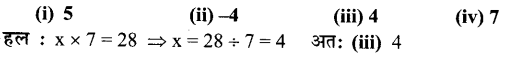
(b) किसी संख्या x में 5 से भाग देने पर भागफल 7 आता है, तो वह संख्या है

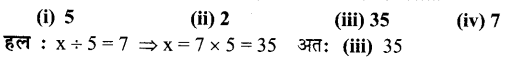
(c) यदि एक विषम संख्या 2x +1 है, तो दूसरी क्रमागत विषम संख्या होगी

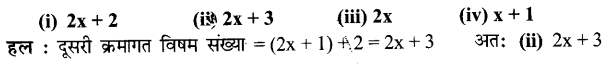
प्रश्न 2.
कुछ गणितीय कथनों को रेखीय समीकरणों के रूप में अभिव्यक्त किया गया है। सही समीकरणों को छाँटिए

प्रश्न 3.
एक संख्या का $\frac { 1 }{ 2 }$ , उसी संख्या के $\frac { 1 }{ 4 }$ से 15 अधिक है, संख्या ज्ञात कीजिए।

प्रश्न 4.
एक संख्या 7 से 4 बड़ी है, वह संख्या बताइए।

प्रश्न 5.
एक कक्षा में 45 विद्यार्थी हैं। यदि छात्रों की संख्या छात्राओं की । हो, तो छात्राओं की संख्या बताइए।

प्रश्न 6.
एक संख्या के $\frac { 1 }{ 3 }$ भाग में क्सका $\frac { 1 }{ 4 }$ भाग घटाने पर 4 शेष है। संख्या बताइए।

प्रश्न 7.
आदर्श, डेविड और हमीद का कुल भार 44 किलोग्राम है। यदि डेविड का भार आदर्श के भार से 1.3 किग्रा अधिक एवं हमीद के भार से 2.1 किग्रा० अधिक हो, तो तीनों का अलग-अलग भार ज्ञात कीजिए।

प्रश्न 8.
दो अंकों की एक संख्या के अंकों का योगफल 4 है। यदि दहाई के अंक से इकाई का अंक घटा दिया जाए, तो शेष 2 है। संख्या ज्ञात कीजिए।

प्रश्न 9.
दो क्रमागत संख्याओं का योगफल 21 है। उन संख्याओं को बताइए।

प्रश्न 10.
दो क्रमागत सम संख्याओं का योगफल 30 है। उन संख्याओं को ज्ञात कीजिए।

प्रश्न 11.
दो क्रमागत विषम संख्याओं को योगफल 40 है। उन संख्याओं को ज्ञात कीजिए।

प्रश्न 12.
एक भिन्न संख्या का हर 7 है। यदि उसके अंश और हर दोनों में 3 जोड़ दिया जाए, तो उस भिन्न का मान $\frac { 4 }{ 5 }$ हो जाता है। वह भिन्न ज्ञात कीजिए।

अभ्यास 6(d)

प्रश्न 1.
माँ की आयु उसके पुत्र की आयु की 5 गुनी है। 8 वर्ष पश्चात् माँ पुत्र की आयु से 3 गुनी हो जाएगी। दोनों की वर्तमान आयु ज्ञात कीजिए।
हल :
माना पुत्र की वर्तमान आयु = x वर्ष

प्रश्न 2.
अब्दुल अपने पिता से 25 वर्ष छोटा है। यदि 10 वर्ष पूर्व पिता की आयु अब्दुल की आयु की छह गुनी रही हो, तो अब्दुल की वर्तमान आयु क्या है?
हल :
माना अब्दुल की वर्तमान आयु = x वर्ष

प्रश्न 3.
माँ की आयु पिता की आयु से 5 वर्ष कम है। 10 वर्ष पूर्व दोनों की आयु का अनुपात 5:6 था। माँ की वर्तमान आयु बताइए।
हल :
माना माँ की वर्तमान आयु = x वर्ष

प्रश्न 4.
माया अपने 5 वर्ष के बच्चे से इस समय 20 वर्ष बड़ी है। अब से कितने वर्ष पश्चात् उसकी आयु बच्चे की आयु की 3 गुनी हो जाएगी?
हल :
बच्चे की वर्तमान आयु = 5 वर्ष

अभ्यास 6(e)

प्रश्न 1.
एक समकोण त्रिभुज के दो न्यूनकोणों का अनुपात 7:11 है। कोणों के मान ज्ञात कीजिए।
हल :
माना त्रिभुज के दो न्यूनकोण = 7 x व 11 x

प्रश्न 2.
दो कोटिपूरक कोणों का अन्तर 20° है। प्रत्येक कोण की माप बताइए।
हल :
माना पहला कोण = x

प्रश्न 3.
दो सम्पूरक कोणों का अन्तर 40° है। प्रत्येक कोण की माप क्या है?
हल :
माना पहला कोण = x

प्रश्न 4.
एक आयताकार मैदान 190 मी लम्बे तार से घिरा है। यदि मैदान की लम्बाई उसकी चौड़ाई की डेढ़ गुनी हो, तो मैदान की लम्बाई और चौड़ाई अलग-अलग ज्ञात कीजिए।
हल :
माना मैदान की चौड़ाई = x मी

अभ्यास 6(f)

प्रश्न 1.
एक मालगाड़ी जिसकी लम्बाई 450 मी है, एक खम्भे को 18 सेकंड में पार करती है, उस मालगाड़ी की चाल किमी प्रति घण्टा में ज्ञात कीजिए।

प्रश्न 2.
1.3 किमी दूर खड़े आदर्श को एक गोले के फटने की आवाज उसके फटने से 4 सेकंड बाद सुनाई पड़ी। ध्वनि की चाल मीटर प्रति सेकंड में ज्ञात कीजिए।

प्रश्न 3.
एक व्यक्ति 15 किमी की दूरी 3 घण्टे में तय करता है जिसमें कुछ दूरी टहलते हुए तथा शेष दूरी दौड़कर तय करता है। यदि उसकी चाल टहलने में 3 किमी प्रति घण्टा तथा दौड़ने में 9 किमी प्रति घण्टा रही हो, तो उसने दौड़कर कितनी दूरी तय की थी?
हल :
माना व्यक्ति द्वारा टहलते हुए तय की गई दूरी = x किमी

प्रश्न 4.
नसरीन घर से 3 किमी प्रति घण्टा की चाल से विद्यालय जाती है और 4 किमी प्रति घण्टा की चाल से वापस आती है। यदि उसे आने-जाने में कुल 21 मिनट लगे, तो उसके घर से विद्यालय कितनी दूरी है?
हल :
माना नसरीन के घर से विद्यालय की दूरी = x किमी
नसरीन द्वारा घर से विद्यालय जाने में लगा समय = घण्टे
नसरीन द्वारा विद्यालय से घर जाने में लगा समय = घण्टे
आने-जाने में लगा कुल समय = 21 मिनट = घण्टे

प्रश्न 5.
संजय साइकिल द्वारा 10 किमी प्रति घण्टा की चाल से कार्यालय 6 मिनट विलम्ब से पहुँचा। यदि वह अपनी चाल 2 किमी प्रति घण्टा बढ़ा देता, तो वह 6 मिनट पहले पहुँच जाता। उसके घर से कार्यालय की दूरी ज्ञात कीजिए।
हल :
माना घर से कार्यालय की दूरी = x किमी

प्रश्न 6.
हामिद के घर से डेविड का घर 19 किमी दूर है। प्रातः 9 बजे वे एक-दूसरे के घर के लिए साइकिल द्वारा प्रस्थान करते हैं यदि हामिद की चाल 9 किमी प्रति घण्टा और डेविड की चाल 10 किमी प्रति घण्टा हो, तो वे दोनों हामिद के घर से कितनी दूरी पर तथा कब मिलेंगे?
हल :
हामिद के घर से डेविड के घर की दूरी = 19 किमी
चूँकि हामिद वे डेविड विपरीत दिशा में जी रहे हैं,
अत: एक-दूसरे के सापेक्ष चाल = 9+ 10 = 19 किमी/घण्टा
दूरी तय करने में लगा समय = दूरी/चाल = = 1 घण्टा
हामिद द्वारा 1 घण्टे में चली दूरी = हामिद की चाल x समय
= 9x 1 = 9 किमी।
अतः दोनों हामिद के घर से 9 किमी की दूरी पर तथा 9+ 1 = 10 बजे प्रातः मिलेंगे।

प्रश्न 7.
सरकार द्वारा अनाथालय के बच्चों को पुष्टाहार देने के लिए 200 ग्राम दलिया प्रति बच्चे की दर से वितरित किया गया। यदि कुल 20 किग्रा० दलिया वितरित हुआ हो तो बच्चों की संख्या कितनी थी?
हल :
कुल दलिया वितरित हुआ = 20 किग्रा० = 20000 ग्राम
1 बच्चे को दलिया मिला = 200 ग्राम
बच्चों की संख्या = = 100

प्रश्न 8.
पन्द्रह अगस्त के उपलक्ष्य में एक स्कूल के बच्चों में कुल ४ किग्रा० सेब वितरित हुआ। सेब का मूल्य रुपये प्रति किग्रॉ० था। फल व्यापारी ने राष्ट्रीय पर्व के सम्मान में 10 रुपया प्रतिकिग्रा० मूल्य कम लिया। सेब का कुल मूल्य 2000 रुपये को भुगतान राशि को समीकरण द्वारा दर्शाइए।
हल :
बच्चों में कुल सेब वितरित हुआ = x किग्रा०
1 किग्रा० सेब का मूल्य था = ₹ m
व्यापारी के 10 रुपये कम करने पर….
1 किग्रा० सेब का मूल्य = ₹ x (m – 10)
x किग्रा० सेब का मूल्य = ₹ x (m – 10)
2000 = ₹ x (m – 10)
अत: x (m – 10) = ₹ 2000

दक्षता अभ्यास 6

प्रश्न 1.
निम्नलिखित समीकरणों को हल कीजिएः

प्रश्न 2.
किसी संख्या के 5 गुने से उसका 3 गुना घटने पर शेषफल 18 है। वह संख्या बताइए।
हल :
मानो वह संख्या = x

प्रश्न 3.
दो क्रमागत विषम संख्ओं का योगफल उसके अन्तर का 6 गुना है। उन संख्याओं को ज्ञात कीजिए।
हल :
माना प्रथम विषम संख्या = x

प्रश्न 4.
एक व्यक्ति एक बाग से कुछ फूल चुनता है। वह इन फूलों का $\frac { 1 }{ 2 }$ भाग माली को, $\frac { 1 }{ 4 }$ भाग फूलदान के लिए, $\frac { 1 }{ 6 }$ है भाग अपने पुत्र को $\frac { 1 }{ 18 }$ भाग अपनी पुत्री को तथा शेष 1 फूल अपनी पत्नी को भेंट करता है। उसने कुल कितने फूल चुने थे?

प्रश्न 5.
रबिया और एबी की आयु में 2 वर्षों का अन्तर है। यदि रबिया की आयु एबी की आयु के 2 गुने से 6 वर्ष कम हो, तो दोनों की आयु ज्ञात कीजिए।
हल :
माना रबिया की आयु = x वर्ष

एबी की आयु = x -2 = 10-2 = 8 वर्ष
अतः रबिया की आयु 10 वर्ष तथा एबी की आयु 8 वर्ष है।

प्रश्न 6.
पिता की आयु उसके पुत्र की आयु की 4 गुनी है। 6 वर्ष बाद पिता की आयु पुत्र की आयु के ढाई गुने से 6 वर्ष अधिक हो जाएगी। दोनों की वर्तमान आयु ज्ञात कीजिए।
हल :
माना पुत्र की वर्तमान आयु = x वर्ष
तथा पिता की वर्तमान आयु = 4x वर्ष
6 वर्ष बाद पुत्र की आयु = (x +6) वर्ष
6 वर्ष बाद पिता की आयु = (4x +6) वर्ष

प्रश्न 7.
एक आयत की लम्बाई उसकी चौड़ाई से 5 सेमी अधिक है। यदि उसका परिमाप 26 सेमी हो, तो उसकी लम्बाई ज्ञात कीजिए।
हल :
माना आयत की चौड़ाई = x सेमी

प्रश्न 8.
एक समान्तर चतुर्भुज की एक भुजा (2x -1) सेमी तथा उसके सामने की भुजा (4x – 6) सेमी है। भुजा की माप बताइए।
हल :
समान्तर चतुर्भुज की एक भुजा = (2x – 1) सेमी

प्रश्न 9.
पाश्र्वांकित चित्र में x का मान ज्ञात कीजिए।

हल :
त्रिभुज के तीनों कोणों का योग = 180°
⇒ x + 40° + 85° = 180°
⇒ x = 180° – 40° – 85° = 180° – 125°
⇒ x = 55°

प्रश्न 10.
एक महिला साइकिल से’ (4x + 1) किमी की दूरी 5 घण्टे में तय करती है। यदि उसकी चाल (x -2) किमी प्रति घण्टा हो, तो तय की गई दूरी ज्ञात कीजिए।
हल :
दूरी = (4x + 1) किमी
समय = 5 घण्टे

प्रश्न 11.
एक लड़का $2\frac { 1 }{ 2 }$ घण्टे में 20 किमी दूरी तय करता है। यदि उसने 5 किमी प्रति घण्टा की चाल से कुछ दूरी पैदल चलकर और शेष दूरी को 10 किमी प्रति घण्टा की चाल से साइकिल द्वारा तय की हो तो उसके द्वारा पैदल चली गई दूरी ज्ञात कीजिए।
हल :
माना लड़का पैदल दूरी तय करता है = x किमी

प्रश्न 12.
जब माधव 12 किमी प्रति घण्टा की चाल से विद्यालय जाता है, तो वह 3 मिनट विलम्ब से पहुँचता है। किन्तु जब वह 16 किमी प्रति घण्टा की चाल से विद्यालय जाता है, तो वह 2 मिनट पहले पहुँचता है। उसके घर से विद्यालय की दूरी ज्ञात कीजिए।
हल :
माना घर से विद्यालय की दूरी = x किमी
12 किमी/घण्टे की चाल से चलकर विद्यालय पहुँचने में लगा समय = $\frac { x }{ 12 }$ घण्टे
16 किमी/घण्टे की चाल से चलकर विद्यालय पहुँचने में लगा समय = $\frac { x }{ 16 }$ घण्टे

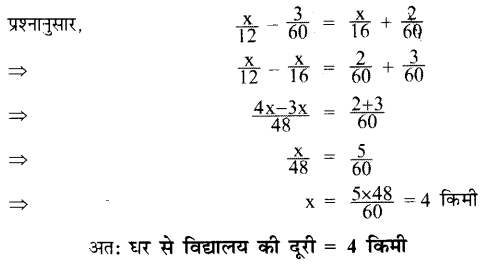
एम.एस.ई

प्रश्न 13.
दो संख्याओं का योगफल 710 है। जब बड़ी संख्या को छोटी संख्या से भाग दिया जाता है, तो भागफल 12 और शेषफल 8 आता है, तो बड़ी संख्या होगी।
(क) 566
(ख) 656
(ग) 665
(घ) 654
हल :
माना छोटी संख्या b है, तो बड़ी संख्या 710 – b होगी।
प्रश्नानुसार, 12b + 8 = 710 – b
13 b = 710 – 8 = 702
b = 54, तो बड़ी संख्या = 710 – 54 = 656 (ख)

प्रश्न 14.
यदि 2 +7= 17, 2z + x = 15 और 2x + y = 10, तो x + y +z का मान होगा।
(क) 42
(ख) 39
(ग) 41
(ग) 14
हल :
(2y + z) + (2z +x) + (2x + y) = 17 + 15 + 10
2y + z + 2z + x + 2x + y = 42
3y + 3z + 3x = 42
= x ÷ y + z = $\frac { 42 }{ 3 }$ = 14 (घ)

We hope the UP Board Solutions for Class 7 Maths Chapter 6 रेखीय समीकरण Ex 6(a) help you.

UP Board Solutions for Class 7 Maths Chapter 6 रेखीय समीकरण

UP Board Solutions for Class 7 Maths Chapter 6 रेखीय समीकरण

Leave a Reply Cancel reply

Recent Posts