UP Board Solutions for Class 6 Maths Chapter 13 त्रिभुज
These Solutions are part of UP Board Solutions for Class 6 Maths. Here we have given UP Board Solutions for Class 6 Maths Chapter 13 त्रिभुज.
अभ्यास 13(a)
प्रश्न 1.
निम्नांकित चित्रों को काटिए, प्रत्येक को दो भागों में इस प्रकार मोड़िए कि दोनों भाग सर्वांगसम हो जाएँ।
उत्तर-
विद्यार्थी चित्रों को काटकर स्वयं मोड़ें।
प्रश्न 2.
नीचे बने चित्रों को यदि बिन्दुदार रेखाओं पर दो भागों में मोड़ा जाए, तो प्रत्येक के दोनों भाग सर्वांगसम हैं या नहीं? अपनी अभ्यास पुस्तिका में प्रत्येक के समक्ष हाँ या नहीं में उत्तर लिखिए-
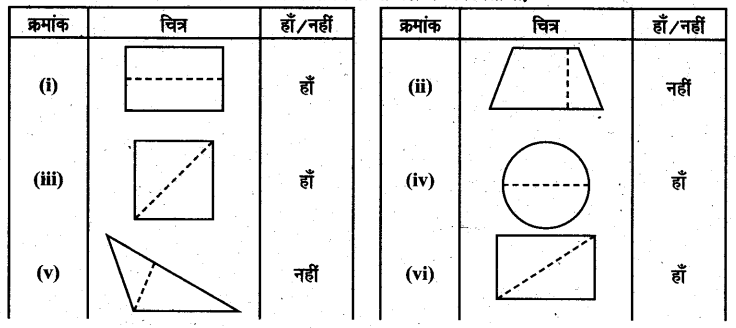

प्रश्न 3.
निम्नलिखित त्रिभुजों को उनके कोणों के आधार पर वर्गीकृत कीजिए। उत्तर

प्रश्न 4.
निम्नलिखित त्रिभुजों को उनके भुजाओं के आधार पर वर्गीकृत कीजिए।

उत्तर-
(i) समद्विबाहु त्रिभुज
(ii) विषमबाहु त्रिभुज
(iii) विषमबाहु त्रिभुज
(iv) समबाहु त्रिभुज
प्रश्न 5.
नीचे दो रेखाखण्ड दिए गए हैं, दोनों रेखाखण्ड सर्वांगसम हैं। यदि AB = 4.5 सेमी, तो CD की लम्बाई कितनी होगी?
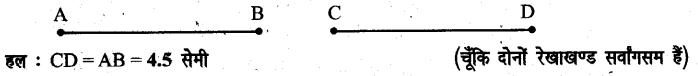
प्रश्न 6.
चित्र में A, B, C, D एक रेखा पर स्थित बिन्दु हैं। रेखाखण्ड CA = रेखाखण्ड BD, तो रेखाखण्ड CB और AD बराबर हैं या नहीं?
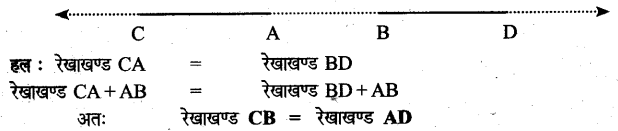

अभ्यास 13(b)
प्रश्न 1.
त्रिभुज ABC की रचना कीजिए जबकि AB = 6 सेमी, BC = 8 सेमी तथा AC = 4 सेमी।
हल:
दिया है- ΔABC में,
AB = 6 सेमी , BC = 8 सेमी तथा AC = 4 सेमी
रचना करनी है- ΔABC की रेखाखण्ड

रचना-
- सर्वप्रथम रेखाखण्ड BC=8 सेमी खींचा।
- बिन्दु B को केन्द्र मानकर 6 सेमी त्रिज्या का एक चाप लगाया।
- बिन्दु C को केन्द्र मानकर 4 सेमी त्रिज्या का एक चाप लगाया।
- दोनों चाप एक दूसरे को बिन्दु A पर काटते हैं। A से B तथा C को मिलाया।
- ΔABC अभीष्ट त्रिभुज है।
प्रश्न 2.
निम्नांकित त्रिभुजों के जोड़ों में भुजाओं की नाप अंकित है। भुजा-भुजा-भुजा सर्वांगसमता प्रतिबंध का प्रयोग करके बताइए, कौन त्रिभुज किस त्रिभुज के सर्वांगसम है, उत्तर को सांकेतिक भाषा में लिखिए।
हल:
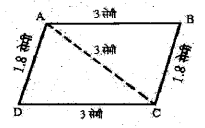
(i) ΔABC तथा ΔCDA में,
भुजा BC = भुजा AD = 1.8 सेमी
भुजा AB = भुजा CD = 3 सेमी
तथा भुजी AC = भुजा AC (उभयनिष्ठ)
अतः ΔABC = ΔCDA
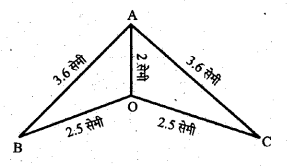
(ii) ΔAOB तथा ΔAOC में,
भुजा AB = भुजा AC = 3.6 सेमी
भुजा OB = भुजा, OC = 2.5 सेमी
तथा भुजा AO = भुजा AO = 2 सेमी (उभयनिष्ठ)
अतः ΔAOB = ΔAOC
(iii) ΔABC तथा ΔPQR में
भुजा AB = भुजा PQ = 1.8 सेमी
भुजा AC = भुजा PR = 2.4 सेमी
तथा भुजा BC = भुजा QR = 2.8 सेमी
अतः ΔABC = ΔPQR

प्रश्न 3.
पाश्वाकित चित्र में AD = DC और AB = BC
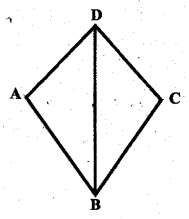
(i) क्या ΔABD = ΔCBD ?
उत्तर-
हाँ, ΔABD = ΔCBD
(ii) यदि ΔABD = ΔCBD, तो इसके संगत भुजाओं और संगत कोणों को लिखिए।
हल:
ΔABD = ΔCBD
भुजा AB = भुजा CB
भुजा AD = भुजां CD
भुजा BD = भुजा BD
∠BAC = ∠BCD
∠CBD = ∠ABD
∠CDB = ∠ADB
प्रश्न 4.
पाश्वाँकित चित्र में ΔABC और ΔABD; एक ही भुजा AB पर बने त्रिभुज हैं। AC = BD तथा BC = AD हैं। निम्नांकित कथन में कौन सत्य/असत्य है?
(i) ΔABC = ΔABD
(ii) ΔABC = ΔADB
(iii) ΔABC = ΔBAD

हल:
AB = AB, AC = BD तथा BC = AD
अतः (iii) ΔABC = ΔBAD सत्य है।
अभ्यास 13(c)
प्रश्न 1.
चित्र में, दो त्रिभुज आपस में सर्वांगसम हैं, उन्हें छाँटकर सांकेतिक भाषा में लिखिए।
हल:

ΔABC तथा ΔHIJ में,
भुजा AB = भुजा HI = 2 सेमी
भुजा AC = भुजा HJ = 3 सेमी
∠CAB = ∠JHI = 30°
अतः ΔABC = ΔHIJ
पुनः ΔRPQ, ΔGEF तथा ΔMKL में
RQ = GF = ML = 3 सेमी
QP = FE = LK = 2 सेमी ।
∠RPQ = ∠GEF = ∠MKL
ΔPRQ = ΔGEF = ΔMKL
प्रश्न 2.
एक त्रिभुज ΔABC की रचना कीजिए, जिसमें AB = 6 सेमी, AC = 6 सेमी और ∠A = 90°, त्रिभुज XYZ की रचना कीजिए जिसमें XY = 6 सेमी, ∠X = 90° और ∠Y = 45° क्या दोनों त्रिभुज सर्वांगसम हैं?
हल:
रचना – 6 सेमी लम्बाई का रेखाखण्ड AB खींचा। बिन्दु A पर चाँदा की। सहायता से 90° कोण बनाती हुई 6 सेमी लम्बाई का रेखाखण्ड AC खींचा।
बिन्दु C और B को मिलाया। ΔABC अभीष्ट त्रिभुज है।
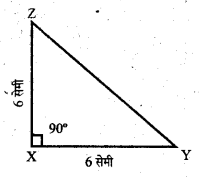
रचना – 6 सेमी लम्बाई का रेखाखण्ड XY खींचा। बिन्दु X पर चॉदा की सहायता से 90° कोण बनाती हुई एक रेखा खींची और बिन्दु Y पर चॉदा की सहायता से 45° कोण बनाती हुई एक रेखा खींची।
जो बिन्दु Z पर मिलती हैं।
ΔXYZ अभीष्ट त्रिभुज है।
ΔABC तथा ΔXYZ में
CA = ZX = 6 सेमी
AB = XY = 6 सेमी
∠CAB = ∠ZXY = 90°
∠ABC = ∠XYZ = 45°
ΔABC = ΔXYZ
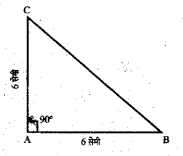
प्रश्न 3.
पाश्वकित चित्र में, AB = AC और ∠DAB = ∠CAD, तो क्या ΔACD और ΔABD सर्वांगसम हैं? यदि हैं तो क्यों?

हुल:
ΔACD तथा ΔABD में,
AC = AB
∠CAD = ∠DAB
तथा AD उभयनिष्ठ है। (SAS)
ΔACD = ΔABD
क्योंकि जिस त्रिभुज की दो भुजा और उनके बीच का कोण दूसरे त्रिभुज के दो भुजाओं और उनके बीच के कोण के अलग-अलग बराबर होते हैं, वे त्रिभुज सर्वांगसम होते हैं।
प्रश्न 4.
त्रिभुज ΔABC की रचना कीजिये जबकि AC = 4.5 सेमी, BC = 6 सेमी तथा ∠C = 60°
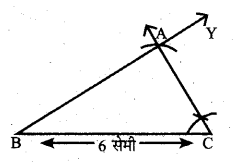
हुल :
दिया है- ΔABC की भुजा
AC = 4.5 सेमी
BC = 6 सेमी
तथा ∠C = 60°
रचना करनी है- ΔABC की
रचना-
- सर्वप्रथम रेखाखण्ड BC = 6 सेमी खींचा।
- बिन्दु C पर पटरी व परकार की सहायता से 60° का कोण बनाती हुई रेखा BY खींची।
- रेखा BY रेखाखण्ड AC = 4.5 सेमी की दूरी पर चिह्न A लगाया।
- A से B को मिलाया।
- यही ΔABC अभीष्ट त्रिभुज है।
अभ्यास 13(d)
प्रश्न 1.
निम्नलिखित त्रिभुजों में कौन-सा त्रिभुज किस त्रिभुज के सर्वांगसम है।

हल:
(i) ΔABC तथा ΔFDE में,
∠A = ∠F = 40° and ∠B = ∠E = 60°
भुजा AB = भुजा EF = 3.5 सेमी
ΔABC = ΔDEL
(ii) ΔABC तथा ΔBAD में,
∠A = ∠B,
25° + 30° = 55° = ∠CAB = ∠DBA = 30°
भुजा AB = भुजा AB (उभयनिष्ठ)
अतः ΔABC = ΔBAD
(iii) ΔODA तथा ΔOBC में,
∠ADO = ∠CBO = 100°
भुजा OD = भुजा OB = 2 सेमी
∠AOD = ∠COB (शीर्षाभिमुख कोण)
अतः ΔODA = ΔOBC
प्रश्न 2.
चित्र में AD, ∠A की अर्धक है, तथा AD ⊥ BC.
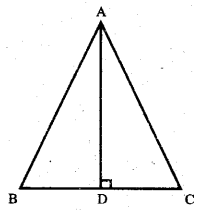
(i) क्या ΔADB = ΔADC
हल:
ΔADB तथा ΔADC में,
∠BAD = ∠CAD
∠ADB = ∠ADC = 90°
भुजा AD = भुजा AD (उभयनिष्ठ)
ΔADB = ΔADC
(ii) क्या यह कहना सही है कि BD = DC?
हल:
ΔADB = ΔADC
BD = DC
प्रश्न. 3.
चित्र में रेखा AX, ∠CAB और ∠BDC को समद्विभाजित करती है। उन तीन तथ्यों को बताइए जो यह सिद्ध करें कि ΔABD = ΔACD

हुल :
ΔABD तथा ΔACD में,
∠CAD = ∠BAD
∠CDA = ∠BDA
भुजा AD = भुजा AD (उभयनिष्ठ)
ΔABD = ΔACD
प्रश्न 4.
त्रिभुज ΔABC की रचना कीजिये जबकि AC = 4.5 सेमी, BC = 6 सेमी तथा ∠C = 60°
हल:
दिया है- ΔABC में रेखाखण्ड AC = 6 सेमी
∠A = 60° तथा ∠C = 45°
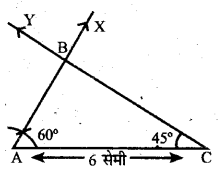
रचना करनी है- ΔABC की
रचना-
- सर्वप्रथम रेखाखण्ड AC=6 सेमी खींचा .
- बिन्दु A पर पटरी व परकार की सहायता से 60° का कोण ब नाती हुई रेखा AX खींची।
- इसी प्रकार बिन्दु C पर पटरी व परकार की सहायता से 45° का कोण बनाती हुई रेखा CY खींची।
- दोनों रेखाएँ AX व CY एक दूसरे को बिन्दु B पर प्रतिच्छेद करती है।
- यही ΔABC अभीष्ट त्रिभुज है।
अभ्यास 13(e)
प्रश्न 1.
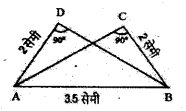
नीचे कुछ त्रिभुज के जोड़े दिए गए हैं। उनकी नाप भुजाओं के साथ लिख दी गई है। ‘समकोण-कर्ण-भुजा सर्वांगसमता का प्रयोग करके बताइए कि कौन-कौन से त्रिभुज सर्वांगसम है? परिणाम को सांकेतिक रूप में लिखिए।
हल:
(i) ΔADB तथा ΔACB में,
AD = BC = 2 सेमी
∠ADB = ∠ACB = 90°
तथा AB = AB = 3.5 सेमी
अतः ΔADB = ΔACB
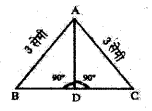
(ii) ΔADB तथा ΔADC में,
AB = AC = 3 सेमी
AD = AD (उभयनिष्ठ)
∠ADB = ∠ADC = 90°
सर्वांगसमता के ‘समकोण-कर्ण-भुजा’ नियम से
ΔADB = ΔADC
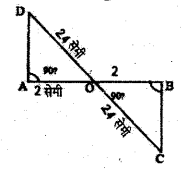
(iii) ΔOAD तथा ΔOBC में,
∠OAD = ∠OBC = 90°
OD = OC = 2.4 सेमी
OA = OB = 2 सेमी
सर्वांगसमता के ‘समकोण-कर्ण-भुजा’ नियम से
ΔOAD = ΔOBC
प्रश्न 2.
BD और CE, ΔABC की भुजाओं AC और AB पर क्रमशः लम्ब खींचे गए हैं और BD = CE

(i) क्या ΔDBC = ΔCBE ?
हल:
∠CEB = ∠BDC = 90°
भुजा BD = भुजा CE (दिया है)।
भुजा BC = भुजा BC (उभयनिष्ठ)
ΔDBC = ΔCBE
(ii) भुजा EB और भुजा CD में क्या सम्बन्ध होगा?
हल:
ΔDBC = ΔCBE
अतः भुजा EB = भुजा CD
प्रश्न 3.
उस प्रतिबंध को अभ्यास पुस्तिका पर लिखिए जबकि दो समकोण त्रिभुज सर्वांगसम होंगे।
उत्तर-
यदि एक समकोण त्रिभुज का कर्ण और एक भुजा दूसरे समकोण त्रिभुज के कर्ण और एक भुजा के बराबर हो, तो दोनों त्रिभुज सर्वांगसम होंगे। इसे ‘समकोण-कर्ण-भुजा’ (R.H.S.) सर्वांगसमता कहते हैं।
प्रश्न 4.
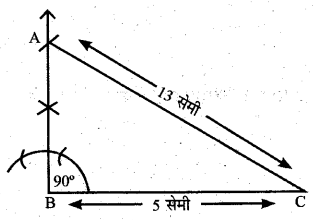
त्रिभुज ΔARC की रचना कीजिये जबकि AC = 13 सेमी, BC = 5 सेमी तथा ∠B = समकोण है। त्रिभुज के तीनों कोणों का योगफले इसे कीजिए तथा निष्कर्ष निकालिए:
हल:
दिया है- ΔABC में रेखाखण्ड AC = 13 सेमी।
BC =5 सेमी तथा ∠B = 90°
रचना करनी है- ΔABC की।
रचना-
- सर्वप्रथम रेखाखण्ड BC = 5 सेमी खींचा।
- बिन्दु B परकार व पटरी की सहायता से 90° का कोण बनाती हुई रेखा BX खींची।
- बिन्दु C रेखाखण्ड AC = 13 सेमी लेकर रेखा BX पर चिह्न A लगाया। A से C को मिलाया।
- अतः यही ΔABC अभीष्ट त्रिभुज है।
अभ्यास 13(f)
प्रश्न 1.
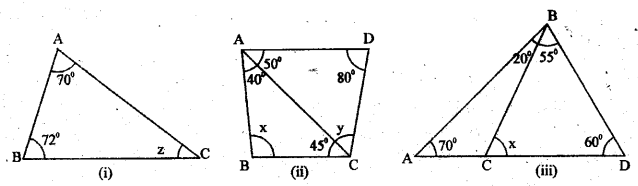
निम्नलिखित प्रश्नों में X, Y, Z का मान निकालिये।
हल:
(i) ∠A = 70°, ∠B = 72°, ∠C = Z
Δ के तीनों अन्तः कोणों का योग 180° होता है।
∠A + ∠B + ∠C = 180
70 + 72 + Z = 180
142 + Z = 180
Z = 180 – 142
Z = 38
अतः ∠Z = 38°
(ii) ΔACD में
∠A = 50°, ∠C = y, ∠D = 80°
∠A + ∠C + ∠D = 180°
50 + y + 80 = 180
130 + y = 180
y = 180 – 130
y = 50
तथा ΔABC में,
∠A = 40°, ∠B = x°, ∠C = 45°
∠A + ∠B + ∠C = 180°
40 + x° + 45 = 180
85 + x = 180
x = 180 – 85
x = 95
(iii) ΔBCD में,
∠CBD = 55°, ∠BDC = 60°, ∠BCD = x
∠CBD + ∠BCD + ∠BDC = 180°
55 + x + 60 = 180
115 + x = 180
x = 180 – 115
x = 65
प्रश्न 2.
चित्रानुसार का मान ज्ञात कीजिए|

हल:
(i) ΔABC में,
∠A = 3x°, ∠B = 60° तथा ∠C = x°
∠A + ∠B + ∠C = 180°
3x° + 60 + x° = 180
4x + 60 = 180
4x = 180 – 60
4x = 120
x = 30°
(ii) ΔABC में,
∠A = 2x°, ∠B = 3x° तथा ∠ACD = 115°
∠ACD, ΔABC के लिए बाह्य कोण है|
∠ACD = ∠CAB + ∠ABC
115 = 2x° + 3x°
5x° = 115
x = 23°
प्रश्न 3.
निम्नलिखित में X, Y का मान ज्ञात कीजिए।

हल:
(i) ∠ABC = x°, ∠ACB = 51°, तथा ∠CAD = 107°
ΔACD में, ∠CAD बाह्य कोण है।
अतः ∠CAD = ∠ABC + ∠ACB
107 = x° + 51°
x = 107 – 51
x = 56°
(ii) ΔACD में, ∠A = x°, ∠B = 40°, ∠C = 107°
∠A + ∠B + ∠C = 180°
x + 40 + 107 = 180
x + 147 = 180
x = 180 – 147
x = 33
तथा
x° + 65 + y° = 180°
33 + 65 + y = 180
98 + y = 180
y = 180 – 98
y = 82
प्रश्न 4.
ΔABC में ∠B = 72°, ∠C = 64°, ∠A का ज्ञात कीजिए।
हल:
ΔABC में ∠B = 72°, ∠C = 64°, ∠A = ?
∠A + ∠B + ∠C = 180°
∠A + 72° + 64° = 180°
∠A + 136° = 180°
∠A = 180° – 136°
∠A = 44°
प्रश्न 5.
यदि किसी त्रिभुज की कोणों में अनुपात 3 : 4 : 5 हो, तो कोणों के ज्ञात कीजिए।
हल:
त्रिभुज के तीनों कोणों का अनुपात 3 : 4 : 5
माना पहला कोण = 3x
दूसरा कोण = 4x
तथा तीसरा कोण = 5x
3x + 4x + 5x = 180°
12x = 180°
x = 15
अतः पहला कोण = 3 x 15 = 45°
दूसरा कोण = 4 x 15 = 60°
तथा तीसरा कोण = 5 x 15 = 75°
दक्षता अभ्यास 13
प्रश्न 1.
चित्र में ΔABD = ΔCDB चित्र को देखकर निम्नांकित वैकल्पिक उत्तरों में से सही उत्तर छाँटकर अभ्यास पुस्तिका पर लिखिए।

(a) ∠A का संगत कोण है –
(i) ∠B
(ii) ∠D
(iii) ∠C
उत्तर-
(iii) ∠C
(b) भुजा AB की संगत भुजा है।
(i) CD
(ii) AD
(iii) BC
उत्तर-
(i) CD
(c) AD की संगत भुजा है-
(i) CB
(ii) CD
(iii) BA
उत्तर-
(i) CB
(d) DB की संगत भुजा है-
(i) BD
(ii) DC
(iii) BC
उत्तर-
(i) BD
प्रश्न 2.
यदि कक्षा 6 के सभी बच्चे 4 सेमी, 5 सेमी और 6 सेमी भुजा वाले एक त्रिभुज की रचना करें, तो क्या । बनने वाले सभी त्रिभुज सर्वांगसम होंगे?
उत्तर-
हाँ, सभी त्रिभुजं सर्वांगसम होंगे।
प्रश्न 3.
यदि ΔABC = ΔPQR तथा AB = 3.2 सेमी, BC = 5 सेमी और CA = 7 सेमी हो, तो ΔPQR की भुजाओं की माप लिखिए?
हल:
ΔABC = ΔPQR
AB = 3.2 सेमी, BC = 5 सेमी और CA = 7 सेमी
चूंकि दोनों त्रिभुज सर्वांगसम हैं अतः संगत भुजाएँ बराबर होंगी।
अतः PQ = AB = 3.2 सेमी QR = BC = 5 सेमी
RP = CA = 7 सेमी.
प्रश्न 4.
एक त्रिभुज की तीनों भुजाएँ दूसरे त्रिभुज की तीनों संगत भुजाओं के बराबर हैं। क्या दोनों त्रिभुज सर्वांगसम हैं?
उत्तर-
हाँ, दोनों त्रिभुज सर्वांगसम हैं।
प्रश्न 5.
एक त्रिभुज के तीनों कोण दूसरे त्रिभुज के तीनों संगत कोणों के बराबर हों, तो क्या दोनों त्रिभुज सदैव सर्वांगसम होते हैं?
उत्तर-
नहीं, दोनों त्रिभुज सर्वांगसम नहीं हैं।
प्रश्न 6.
एक त्रिभुज का एक कोण 130° का है, शेष दो कोण आपस में बराबर हैं। इन दोनों कोणों की माप ज्ञात कीजिए।
हल:
माना त्रिभुज के दोनों बरोबर कोण = x°
त्रिभुज के तीनों कोणों का योग = 180°
अतः x + x + 130° = 180°
2x = 180° – 130°
2x = 50°
x = 50°
x = 25°
अतः त्रिभुज के शेष दोनों कोण = 25°, 25°
प्रश्न 7.
एक समकोण त्रिभुज के दो कोण बराबर हैं, दोनों कोण कितने-कितने अंश के हैं?
हल:
माना समकोण त्रिभुज के दोनों कोण = x°
अतः
x + x + 90° = 180°
2x = 180° – 90°
2x = 90°
x = 45०
अतः शेष दोनों कोण = 45°, 45°
प्रश्न 8.
पाश्वाकित चित्र में, बिन्दु D, E, त्रिभुज ABC की भुजा AB और AC पर इस प्रकार स्थित है कि DE || BC, यदि ∠B = 30°, ∠A = 40°, तो कोण x, y, z के मान ज्ञात कीजिए।

हल:
∠x° = 30° (संगत कोण)
ΔADE में,
∠x° + ∠z° + 40° = 180°
30° + ∠z° + 40° = 180°
∠z° + 70° = 180°
∠z° = 180° – 70°
∠z° = 110°
अतः ∠y° = ∠z° = 110° (संगत कोण)
प्रश्न 9.
पाश्र्वांकित चित्र में ∠C समकोण हैं। CD ⊥ AB है। ∠A = 65°, तो निम्नांकित कोणों के मान ज्ञात कीजिए।

(i) ∠ACD
(ii) ∠BCD
(iii) ∠CBD
हल:
(i) ΔCAD में
∠CAD + ∠CDA + ∠ACD = 180°
अतः 65° + 90° + ∠ACD = 180°
155° + ∠ACD = 180°
∠ACD = 180° – 155°
∠ACD = 25°
(ii) ΔABC में,
∠ACD + ∠BCD = 90°
25° + ∠BCD = 90°
∠BCD = 90° – 25°
अंतः ∠BCD = 65°
(iii) ΔBCD में,
∠BCD + ∠CDB + ∠CBD = 180°
65° + 90° + ∠CBD = 180°
155° + ∠CBD = 180°
∠CBD = 180° – 155°
∠CBD = 25°
We hope the UP Board Solutions for Class 6 Maths Chapter 13 त्रिभुज help you. If you have any query regarding UP Board Solutions for Class 6 Maths Chapter 13 त्रिभुज, drop a comment below and we will get back to you at the earliest.