These Solutions are part of UP Board Solutions for Class 6 Maths. Here we have given UP Board Solutions for Class 6 Maths Chapter 12 वाणिज्य गणित.

अभ्यास 12(a)

प्रश्न 1.
निम्नलिखित प्रश्नों को अपनी अभ्यास पुस्तिका में लिखिए और रिक्त स्थानों की पूर्ति कीजिए-
हल:
(i) 3 का 4 से अनुपात = 3 : 4
(ii) 5 का 3 से अनुपात = 5 : 3
(iii) 2 को 7 से अनुपात = 2 : 7
(iv) 4 का 7 से अनुपात = 4 : 7

प्रश्न 2.
अनुपात में व्यक्त कीजिए-
(i) 2 किग्रा का 500 ग्राम से
हल:
2000 गाम का 500 ग्राम से
2000 : 500 या 4 : 1
(ii) 5 का 12 से
हल:
5 : 12
(iii) 13 को 75 से
हल:
13 : 75
(iv) 108 का 125 से
हल:
108 : 125

प्रश्न 3.
निम्नांकित तालिका को अपनी अभ्यास पुस्तिका में लिखिए और रमेश तथा सीमा के प्रत्येक विषय के प्राप्तांकों को अनुपात में लिखिए (लिखकर)-
हल:

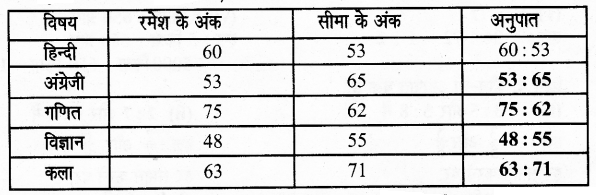
प्रश्न 4.
एक आयताकार खेत की लम्बाई 29 मीटर और चौड़ाई 25 मीटर है। खेत की लम्बाई और चौड़ाई को अनुपात के रूप में लिखिए।
हल:
खेत की लम्बाई और चौड़ाई का अनुपात = 29 : 25प्रश्न 5.
निम्नांकित सारणी को अभ्यास पुस्तिका में लिखिए और रिक्त स्थानों की पूर्ति कीजिए-
हल:

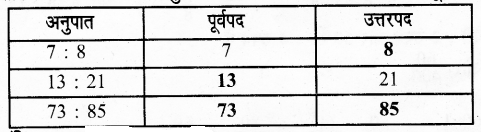
प्रश्न 6.
निम्नांकित अनुपातों के व्युत्क्रम लिखिए-
(i) 3 : 14
(ii) 15 : 17
(iii) 25 : 37
(iv) 65 : 67
हल:
(i) 14 : 3
(ii) 17 : 15
(iii) 37 : 25
(iv) 67 : 65

प्रश्न 7.
प्रथम पद और द्वितीय पद बताइए (बताकर)-
हल:

अभ्यास 12(b)

प्रश्न 1.
आकृति को देखकर अनुपात निकालिए-

(क) आयत के अन्दर के सभी त्रिभुजों की संख्या का वृत्तों की संख्या से।

(ख) आयत के अन्दर के सभी वर्गों की संख्या को सभी आकृतियों से।
(ग) आयत के अन्दर के सभी वृत्तों का सभी आकृतियों से।
उत्तर-
(क) त्रिभुजों की संख्या तथा वृत्तों की संख्या का अनुपात = 3 : 2
(ख) वर्गों की संख्या तथा सभी आकृतियों की संख्या का अनुपात = 2 : 7
(ग) वृत्तों तथा आकृतियों की संख्या का अनुपात = 2 : 7

प्रश्न 2.
सरलतम रूप में अनुपात ज्ञात कीजिए:
(i) 2 का 4 से
हल:
2 : 4 = 1 : 2

(ii) 15 को 3 से।
हल:
15 : 3 = 5 : 1

(iii) 3.5 का 105 से
हल:
3.5 : 105 = 1 : 30

(iv) 50 पैसे का 3 रुपये से
हल:
50 पैसे : 3 रुपये = 50 : 300 = 1 : 6

(v) 2 मीटर का 6 सेमी से
हल:
2 मीटर : 6 सेमी = 200 सेमी : 6 सेमी = 100 : 3

(vi) 2 घंटे का 30 मिनट से
हल:
2 घंटे : 30 मिनट = 120 मिनट : 30 मिनट = 4 : 1

प्रश्न 3.
निम्नांकित अनुपातों को सरलतम रूप में लिखिए (लिखकर)-
(i) 2 : 16
हल:
2 : 16 = 1 : 8

(ii) 18 : 90
हल:
18 : 90 = 1 : 5

(iii) 11 : 121
हल:
11 : 121 = 1 : 11

(iv) 13 : 39
हल:
13 : 39 = 1 : 3
(v) 36 : 72
हल:
36 : 72 = 1 : 2
(vi) 5 किग्रा : 650 ग्राम
हल:
5 किग्रा : 650 ग्राम = 5000 किग्रा : 650 किग्रा = 100 : 13

प्रश्न 4.
कौन-सा अनुपात बड़ा है?

प्रश्न 5.
निम्नांकित कथनों को अनुपात में व्यक्त कीजिए-
(i) एक खेत की लम्बाई उसकी चौड़ाई की चार गुनी है।
हल:
माना खेत की चौड़ाई = x
प्रश्नानुसार, खेत की लम्बाई = 4x
अतः लम्बाई : चौड़ाई = 4x : x = 4 : 1

(ii) मोहन की आयु अपने पुत्र राजेश की आयु की तीन गुनी है।
हल:
माना राजेश की आयु = x
प्रश्नानुसार,
मोहन की आयु = 3x
अतः मोहन की आयु : राजेश की आयु = 3x : x = 3 : 1

(iii) गणित विषय में उत्तीर्ण कक्षा 6 के छात्रों की संख्या, सम्मिलित छात्रों की संख्या की तीन चौथाई है।
हल:
माना सम्मिलित छात्रों की संख्या = x
प्रश्नानुसार,
उत्तीर्ण छात्रों की संख्या = x
अतः उत्तीर्ण छात्रों की संख्या : सम्मिलित छात्रों की संख्या = x : x
= : 1 = 3 : 4

प्रश्न 6.
(a) एक विद्यालय के कक्षा 6 में 100 बच्चे पढ़ते हैं। इनमें 40 लड़के तथा शेष लड़कियाँ हैं। ज्ञात कीजिए।
(i) लड़के और लड़कियों की संख्या का अनुपात।
हल:
विद्यालय में कुल बच्चों की संख्या = 100
विद्यालय में लड़कों की संख्या = 40
अतः विद्यालय में लड़कियों की संख्या = 100 – 40 = 60
लड़के तथा लड़कियों की संख्या का अनुपात = 40 : 60 = 2 : 3

(ii) लड़कों की संख्या और कुल बच्चों की संख्या में अनुपात।
हल:
लड़कों तथा कुल बच्चों की संख्या का अनुपात = 40 : 100 = 2 : 5

(b) एक विद्यालय में 200 बच्चे पढ़ते हैं, जिनमें से 60 बच्चे प्रदूषित जल पीने से बीमार पड़ गए, तो स्वस्थ और बीमार बच्चों की संख्या में अनुपात ज्ञात कीजिए।
हल:
विद्यालय में कुल बच्चों की संख्या = 200
बीमार बच्चों की संख्या = 60
स्वस्थ बच्चों की संख्या = 200 – 60 = 140
स्वस्थ और बीमार बच्चों की संख्या का अनुपात = 140 : 60 = 7 : 3

प्रश्न 7.
अभिनव की आय 5000 रु० प्रतिमाह है। वह 3000 रुपये प्रतिमाह व्यय कर देता है। अनुपात ज्ञात कीजिए।
(i) अभिनव की आय और व्यय में।
हल:
अभिनव की आय = 5000 रु० प्रतिमाह
प्रतिमाह व्यय = 3000 रु०
अतः अभिनव की बचत = 5000 – 3000 = 2000
अभिनव की आय तथा व्यय में अनुपात = 5000 : 3000 = 5 : 3

(ii) अभिनव की व्यय और आय में।
हल:
अभिनव की व्यय तथा आय में अनुपात = 3000 : 5000 = 3000 = 3 : 5

(iii) अभिनव की व्यय और बचत में।
हल:
अभिनव की व्यय तथा बचत में अनुपात = 3000 : 2000 = 3 : 2

प्रश्न 8.
निम्नांकित को अभ्यास पुस्तिका पर लिखिए और फिर रिक्त स्थानों की पूर्ति कीजिए।
हल:

प्रश्न 9.
निम्नांकित चित्रों में छायांकित भाग का अछायांकित भाग के अनुपात को सरलतम रूप में लिखिए-

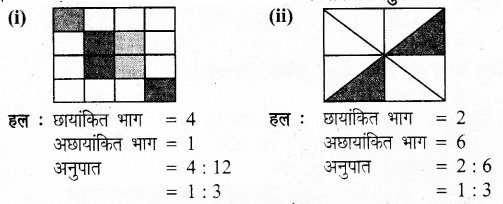
प्रश्न 10.
सुहानी और पलक के बीच 80 को 3 : 2 में बाँटिए।
हल:
सुहानी और पलक का अनुपात = 3 : 2
अनुपातिक योग = 3 + 2 = 5
कुल रुपये = 80
सुहानी को मिले = 80 x = ₹ 48
पलक को मिले = 80 x = ₹ 32

प्रश्न 11.
एक महिला अपनी बेटी श्रेया और भूमिका में 3600 को उनकी आयु के अनुसार बाँटना चाहती है। यदि श्रेया की आयु 15 वर्ष और भूमिका की आयु 12 वर्ष हो तो श्रेया और भूमिका को कितने-कितने रुपये मिलेंगे।
हल:

अभ्यास 12(c)

निम्नालिखित प्रश्न संख्या 1 व 2 में चार-चार उत्तर दिए गए हैं। सही उत्तर अपनी उत्तर-पुस्तिका में लिखिए।
प्रश्न 1.
समानुपाती पदों 20 : 30 :: 60 : 90 में-
(i) 20 और 60 मध्यपद हैं।
(ii) 30 और 90 बाह्यपद हैं।
(iii) 20 और 30 बाह्यपद हैं।
(iv) 30 और 60 मध्यपद हैं।
उत्तर-
(iv) 30 और 60 मध्यपद हैं।

प्रश्न 2.
25, 75, 500, 1000 समानुपात में नहीं है क्योंकि-
(i) यहाँ कोई बाह्य पद नहीं है।
(ii) बाह्य पदों का गुणनफल = मध्य पदों का गुणनफल नहीं है।
(iii) बाह्य पदों का गुणनफल = मध्य पदों का गुणनफल
(iv) मध्य पदों को गुणनफल 3750 हैं।
उत्तर-
(ii) बाह्य पदों का गुणनफल = मध्य पदों का गुणनफल नहीं है।

प्रश्न 3.
नीचे लिखे समानुपाती पदों में x का मान लिखिए-

प्रश्न 4.
निम्नांकित कथन सत्य हैं या असत्य, लिखिए (लिखकर)-
(i) 1 : 2 :: 2 : 4 (सत्य)
(ii) अनुपात 3 : 4 और अनुपात 3 : 5 समानुपात में हैं। (असत्य)
(ii) 3 पुस्तकें : 12 भैंसें :: 4 गायें : 16 कलमें। (सत्य)
(iv) चार पद समानुपात में तभी होंगे, जब चरम पदों को गुणनफल = मध्य पदों का गुणनफल (सत्य)

प्रश्न 5.
एक आयताकार कमरे की लम्बाई और चौड़ाई में 5 : 4 का अनुपात है। यदि कमरे की लम्बाई 15 मीटर हो तो चौड़ाई बताइए।
हल:
कमरे की लम्बाई तथा चौड़ाई का अनुपात = 5 : 4
कमरे की लम्बाई = 15 मी
माना कमरे की चौड़ाई = x
5 : 4 :: 15 : x
5 x x = 4 x 15
x =
x = 12 मी

प्रश्न 6.
15 अगस्त को विद्यालय में बाँटने के लिए लड्डू बनवाया गया। लड्डू बनाने में प्रयुक्त बेसन और चीनी में 1 : 3 का अनुपात है। यदि बेसन कुल 21 किग्रा लगा हो तो चीनी की मात्रा बताइए।
हल:
लड्डू बनाने के लिए बेसन तथा चीनी का अनुपात = 1 : 3
बेसन की मात्रा = 21 किग्रा
माना चीनी की मात्रा = x किग्रा
1 : 3 :: x : 21
1 x 21 = 3 x x
x = = 7 किग्रा

प्रश्न 7.
यदि 6, 18, x, 15 समानुपात में हैं तो ४ का मान क्या होगा?
हल:
6: 18 :: x : 15
6 x 15 = 18 x x
x = = 5

प्रश्न 8.
लखनऊ से कानपुर की दूरी और लखनऊ से इलाहाबाद की दूरी में 3 : 8 का अनुपात हो और लखनऊ से इलाहाबाद के बीच की दूरी 200 किमी हो तो लखनऊ से कानपुर के बीच की दूरी क्या होगी?
हल:
लखनऊ से कानपुर तथा लखनऊ से इलाहाबाद के बीच की दूरी में अनुपात = 3 : 8
तथा लखनऊ से इलाहाबाद के बीच की दूरी = 200 किमी
माना लखनऊ से कानपुर के बीच की दूरी = x
अतः
3 : 8 :: x : 200
3 x 200 = 8 x x
x = = 75 किमी

प्रश्न 9.
एक विद्यालय के लड़के और लड़कियों ने अलग-अलग 2 : 3 के अनुपात में पौधे लगाए। यदि विद्यालय मैं कुल 1500 पौधे लगाए गए हों तो लड़के और लड़कियों द्वारा लगाए गए पौधों की संख्या अलग-अलग निकालिए।
हल:
लड़के और लड़कियों के द्वारा लगाए गए।
पौधों में अनुपात = 2 : 3
तथा विद्यालयों में लगाए गए कुल पौधों की संख्या = 1500
अनुपाती योग = 2 + 3 = 5
लड़कों द्वारा लगाए गए पौधों की संख्या = = 600 पौधे
लड़कियों द्वारा लगाए गए पौधों की संख्या = = 900 पौथे।
अतः लड़कों ने 600 पौधे तथा लड़कियों ने 900 पौधे लगाए।

प्रश्न 10.
गौरव ने 70 रुपये में 10 किग्रा अमरूद बेचे तथा आरिफ ने 5 किग्रा अमरूद 35 रुपये में बेचे। किसका अमरूद सस्ता है? यदि ऐसा है तो वे किस भाव में अमरूद बेच रहे हैं? क्या दोनों अमरूद एक ही भाव में बेच रहे हैं?
हल:
गौरव और आरिफ द्वारा खरीदे गए अमरूद को अनुपात में लिखने पर = 10 किग्रा : 70 रुपये :: 5 किंग्रो 35 रुपये
= 1 : 7 :: 1 : 7
दोनों ने अमरूद 1 रुपये प्रति किग्रा बेचे।
ये दोनों अमरूद एक ही भाव में बेच रहे हैं।

अभ्यास 12(d)

प्रश्न 1.
निम्नांकित में 100 के आधार पर प्रतिशतता बताइए (बताकर)-
(i) 18%
(ii) 24%
(iii) 47%
(iv) 63%
उत्तर-
(i) 18
(ii) 24
(iii) 47
(iv) 63

प्रश्न 2.
निम्नांकित को भिन्न के सरलतम रूप में लिखिए (लिखकर)-

प्रश्न 3.
प्रतिशत में प्रदर्शित कीजिए-
(i) (ii)

प्रश्न 4.
नीचे की तालिका में रिक्त स्थानों की पूर्ति कीजिए (पूर्ति करके)-
हल:

अभ्यास 12(e)

प्रश्न 1.
निम्नलिखित को दशमलव में बदलिए-

प्रश्न 2.
निम्नलिखित को प्रतिशत में बदलिए-

प्रश्न 3.
नीचे दी गई तालिका में रिक्त स्थानों की पूर्ति अपनी पुस्तिका में कीजिए (पूर्ति करके)-
हल:

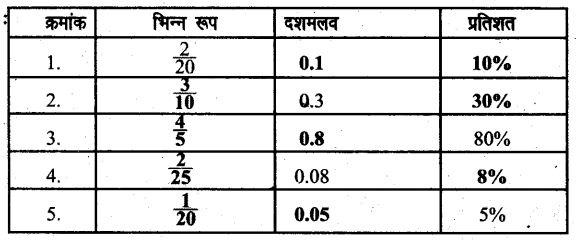
अभ्यास 12(f)

प्रश्न 1.
कितना होगा?

प्रश्न 2.
कितने प्रतिशत होगा?

प्रश्न 3.
एक परीक्षा में 75% बच्चे उत्तीर्ण हुए। यदि परीक्षा में 1500 बच्चे बैठे हों तो कुल कितने बच्चे उत्तीर्ण हुए?
हल:
उत्तीर्ण बच्चों की संख्या = 1500 x = 15 x 75 = 1125 बच्चे

प्रश्न 4.
एक विद्यालय में 2800 बच्चे हैं। उनमें से 980 लड़कियाँ हैं। विद्यालय में कितने प्रतिशत लड़के हैं?
हल:
विद्यालय में लड़कों की संख्या = 2800 – 980 = 1820
लड़कों का प्रतिशत = x 100 = 65%

प्रश्न 5.
एक रिपोर्ट के अनुसार ग्रामीण क्षेत्रों में बच्चों के लिए घातक 10 बीमारियों में से 5 बीमारियाँ प्रदूषित जल के कारण होती हैं, तो बताइए कितने प्रतिशत बीमारियाँ प्रदूषित जल के कारण होती हैं।
हल:
प्रदूषित जल के कारण होने वाली बीमारियों का प्रतिशत = 100 x = 5 x 10 = 50%

प्रश्न 6.
किसी विद्यालय में 400 बालिकाएँ हैं, किन्तु स्वच्छता सम्बन्धी सुविधा न होने के कारण लगभग 12 प्रतिशत बालिकाएँ विद्यालय छोड़ देती हैं, तो बताइए कितनी बालिकाएँ विद्यालय भेड़ देती हैं?
हल:
विद्यालय की कुल बालिकाओं की संख्या = 400
विद्यालय छोड़ चुकी बालिकाओं को प्रतिशत = 12%
विद्यालय छोड़ चुकी बालिकाओं की संख्या = 400 का 12% = 400 x = 48 बालिकाएँ

प्रश्न 7.
एक रक्तदान शिविर में किसी क्षेत्र विशेष के 300 सदस्य स्वेच्छा से रक्तदान करते हैं। यदि उस क्षेत्र की कुल जनसंख्या के केवल 30 प्रतिशत लोगों ने ही रक्तदान किया हो, तो रक्तदान न करने वाले लोगों की संख्या ज्ञात कीजिए।
हल:
माना, क्षेत्र की कुल जनसंख्या = x
कुल जनसंख्या का 30 प्रतिशत = 300
x = = 1000
30 रक्तदान न करने वाले लोगों की संख्या = 1000 – 300 = 700

प्रश्न 8.
ग्रामीण शौचालय निर्माण योजनान्तर्गत सरकार गरीबी रेखा के नीचे के प्रति परिवार को है ₹ 9000 का अनुदान दे रही है। यदि किसी गाँव में इस योजना के अन्तर्गत कुल ₹ 3,60,000 वितरित किए गए हों, तो उस गाँव में कितने परिवार लाभान्वित हुए, जबकि उस गाँव में कुल 200 परिवार निवास करते हैं।
हल:
₹ 3,60,000 में से प्रत्येक परिवार को मिले रुपए = 9000
लाभान्वित परिवार की संख्या = = 40
गाँव के कुल परिवारों की संख्या = 200
लाभान्वित परिवार का प्रतिशत = x 100 = 20%

प्रश्न 9.
किसी नगरपालिका में कुल 40 वार्ड हैं। पूरे नगर में मच्छर उन्मूलन योजनान्तर्गत, फागिंग पर प्रतिवर्ष न प्रतिवार्ड में ₹ 2500 व्यय करने का प्राविधान है। यदि सामान्य स्वास्थ्य पर एक करोड़ रुपये की बचत स्वीकृत हो, तो मच्छर उन्मूलन पर इस स्वीकृत राशि का कितने प्रतिशत धन खर्च किया जा रहा है?
हल:
सभी वार्डों में मच्छर उन्मूलन पर खर्च होने वाली राशि = 40 x 2500 = ₹ 1,00,000
स्वीकृत राशि में से खर्च होने वाली राशि को प्रतिशत = x 100 = 1%

प्रश्न 10.
एक बालिका विद्यालय की 16% बालिकाएँ रक्ताल्पता से पीड़ित हैं। यदि किसी माह में स्वास्थ्य विभाग बारा ऐसी बालिकाओं को 30 गोलियाँ प्रति बालिका की दर से आयरन की कुल 1920 गोलियाँ वितरित की गई, तो विद्यालय में शिक्षा ग्रहण करने वाली सभी बालिकाओं की संख्या क्या है?
हृल:
1920 गोलियों में से प्रत्येक बालिका को मिली गोलियों की संख्या = 30
गोलियाँ पाने वाली बालिकाओं की संख्या = = 64
माना, विद्यालय में शिक्षा ग्रहण करने वाली सभी बालिकाओं की संख्या = x
x का 16% = 64
x x = 64
x = 64 x 100 = 400

अभ्यास 12(g)

प्रश्न 1.
कितना होगा?

प्रश्न 2.
चित्र को देखिए और बताइए (बताकर)-

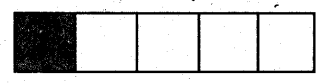
(i) छायांकित भाग पूरे का कौन-सा भाग है?
हल:
छायांकित भाग पूरे का भाग है।

(ii) छायांकित भाग पूरे का कितने प्रतिशत है?
हल:
छायांकित भाग पूरे का 20 प्रतिशत है।

प्रश्न 3.
निम्नलिखित को प्रतिशत में बदलिए-

प्रश्न 4.
निम्नांकित दशमलव भिन्न में बदलिए-

प्रश्न 5.
रिक्त स्थानों की पूर्ति अपनी उत्तर पुस्तिका में कीजिए (पूर्ति करके)-
उत्तर-

प्रश्न 6.
कितना प्रतिशत होगा?

प्रश्न 7.
एक टेम्पो 25 किमी प्रति घंटा की चाल से जा रहा था। उसकी चाल 5%बढ़ गई। अब उसकी चाल होगी-
(क) 30 किमी प्रति घंटा
(ख) 105 किमी प्रति घंटा
(ग) 26.25 किमी प्रति घंटा
(घ) 23.75 किमी प्रति घंटा
हल:
टेम्पो की चाल = 25 किमी प्रति घंटा
चाल में वृद्धि = 25 किमी प्रति घंटा का 5% = 25 x = 1.25 किमी/घंटा
अतः अब टेम्पो की चाल = (25 + 1.25) = 26.25 किमी/घंटा (ग)

प्रश्न 8.
अप्रैल माह की 10 तारीख को तापमान 40°C था। अगले दिन बरसात होने के कारण 30% ताप गिर गया। अब तापमान होगा-
(क) 70°C
(ख) 10°C
(ग) 12°C
(घ) 28°C
हल:
अप्रैल माह की 10 तारीख को तापमान = 40°C
ताप में कमी = 40°C का 30% = 40°C x = 12°C
अब तापमान = 40°C – 12°C = 28°C (घ)

प्रश्न 9.
एक वस्तु का मूल्य ₹ 800 था। इसमें 8% की कमी हो गई। अब नया मूल्य होगा-
(क) ₹ 64
(ख) ₹ 736
(ग) ₹ 864
(घ) ₹ 792
हल:
वस्तु का मूल्य = ₹ 800
वस्तु के मूल्य में कमी = ₹ 800 का 8% = 800 x = 64 रु०
अतः वस्तु का नया मूल्य = 800 – 64 = ₹ 736 (ख)

प्रश्न 10.
एक गाँव में 15% लोग निरक्षर हैं। यदि गाँव की जनसंख्या 2400 हो, तो गाँव में कुल कितने लोग निरक्षर हैं?
हल:
गाँव की जनसंख्या = 2400
गाँव के निरक्षर लोगों का प्रतिशत = 15%
निरक्षर लोगों की संख्या = 2400 x = 360

प्रश्न 11.
रहीम ने गणित में 50 में से 33 अंक प्राप्त किए तथा हिन्दी में 60 में से 36 अंक। रहीम को किस विषय में अच्छे अंक मिले?
उत्तर-
गणित में पूर्णांक = 50
गणित में प्राप्तांक = 33
गणित में प्राप्तांकों का प्रतिशत = x 100 = 66%
हिन्दी में पूर्णांक = 60
हिन्दी में प्राप्तांक = 36
हिन्दी में प्राप्तांकों का प्रतिशत = x 100 = 60%
अतः रहीम को गणित में अच्छे अंक मिले।

प्रश्न 12.
एक गाँव में 2500 पुरुष और 2400 महिलाएँ हैं। दूसरे गाँव में 4000 पुरुष और 3600 महिलाएँ। हैं। किस गाँव में महिलाओं का प्रतिशत अधिक है?
हल:
पहले गाँव में पुरुषों की संख्या = 2500
पहले गाँव में महिलाओं की संख्या = 2400
पहले गाँव की कुल जनसंख्या = 2500 + 2400 = 4900
पहले गाँव में महिलाओं का प्रतिशत = x 100 = 48.98%
दूसरे गाँव में पुरुषों की संख्या = 4000
दूसरे गाँव में महिलाओं की संख्या = 3600
दूसरे गाँव की कुल जनसंख्या = 4000 + 3600 = 7600
दूसरे गाँव में महिलाओं का प्रतिशत = x 100 = 47.37%
अतः हल्ले आँव में महिलाओं का प्रतिशत दूसरे गाँव की अपेक्षा अधिक है।

प्रश्न 13.
अकरम ने एक विषय में 20 में से 12 अंक पत किए। उसने कितने प्रतिशत अंक प्राप्त किए?
हल:
विषय में पूर्णांक = 20
विषय में प्राप्तांक = 12
विषय में प्राप्तांकों का प्रतिशत = x 100 = 60%

प्रश्न 14.
एक उद्यान में 37.5% पेड़ जामुन के हैं। शेष पेड़ आम के हैं। यदि उद्यान में पेड़ों की कुल संख्या 400 हो, के आम के पेॐ की संख्या कितनी होगी?
हल:
उद्यान में जामुनं के पेड़ों का प्रतिशत = 37.5%
उद्यान में आम के पेड़ों का प्रतिशत = 100 – 37.5% = 62.5%
उद्यान के कुल पेड़ों की संख्या = 400
अतः उद्यान में आम के पेड़ों की संख्या = 400 का 62.5% = 400 x = 250

प्रश्न 15.
मदन ने बाजार से 90 सेब खरीदे। यदि 20% सेब खराब निकल गए, तो कितने अच्छे सेब बचे?
हल:
कुल सेबों की संख्या = 90
खराब सेबों का प्रतिशत = 90 का 20%
खराब सेबों की संख्या = 90 x = 18
अच्छे सेबों की संख्या = 90 – 18 = 72 सेब

प्रश्न 16.
एक शिविर में 600 सैनिक थे। 60 सैनिक और आ गए। सैनिकों में कितने प्रतिशत की वृद्धि हो गईं?
हल:
पूर्व सैनिकों की संख्या = 600
नए सैनिकों की संख्या = 60
पहले वाले सैनिकों में प्रतिशत वृद्धि = x 100 = 10%

प्रश्न 17.
एक खंभा 16 मीटर लम्बा है। इसका 40% भाग लाल, 25% भाग काला और शेष भाग पीला रँगा है। पीला रँगा हुआ भाग कितने मीटर होगा ?
हल:
खंभे की लम्बाई = 16 मीटर
पीले भाग का प्रतिशत = 100 – (40% + 25%) = 100 – 65 = 35%
पीले भाग की लम्बाई = 16 मीटर 35% = 16 x = 5.6 मीटर

प्रश्न 18.
एक गाँव की जनसंख्या में 12% की कमी हो जाती है। यदि गाँव की जनसंख्या 25000 हो, तो जनसंख्या में कमी होने के बाद गाँव में कितने लोग होंगे?
हल:
गाँव की जनसंख्या = 25000
गाँव की जनसंख्या में प्रतिशत कमी = 12%
गाँव की जनसंख्या में कमी = 25000 का 12% = 25000 x = 3000
जनसंख्या में कमी होने के बाद गाँव में लोग = 25000 – 3000 = 22000

प्रश्न 19.
एक चुनाव क्षेत्र में 80,000 मतदाता थे। दो प्रत्याशियों में से एक प्रत्याशी को डाले गए मतों का 60% मत मिले। यदि कुल 80% मत पड़े हों, तो दूसरे प्रत्याशी को कितने मत मिले?
हल:
चुनाव क्षेत्र में कुल मतदाता = 80,000
कुल मत पड़े = 80%
मतों की संख्या = 80,000 का 80% = 80000 x = 64000
दूसरे प्रत्याशी का मत प्रतिशत = 100% – 60% = 40%
दूसरे प्रत्याशी को मत मिले = 64000 का 40% = 64000 x = 25600

प्रश्न 20.
एक छड़ 72 सेमी लम्बी थी। इसमें से 9 सेमी काटकर बँटी बना दी गयी। छड़ अब कितने प्रतिशत छोटी हो गई?
हल:
छड़ की लम्बाई = 72 सेमी
छड़ में से बँटी काटी = 9 सेमी
छड़ छोटी हो गई = x 100 = = 12.5%

प्रश्न 21.
एक विद्यालय में कक्षा 6 के बच्चों की संख्या विद्यालय के कुल बच्चों की संख्या का 15% है। यदि कक्षा 6 के बच्चों की संख्या 51 हो, तो विद्यालय में कुल कितने बच्चे हैं?
हल:
विद्यालय में कक्षा 6 के बच्चों का प्रतिशत = 15%
विद्यालय में कक्षा 6 के बच्चों की संख्या = 51
माना विद्यालय में कुल बच्चे x हैं।
प्रश्नानुसार,
x का 15% = 51
x x = 51
x = = 340
विद्यालय में कुल बच्चे = 340

प्रश्न 22.
ग्रामीण विद्युतीकरण परियोजना के अन्तर्गत किसी मलिन बस्ती में प्रति परिवार 2 बल्ब जलाने और एक पंखा चलाने पर प्रतिमाह बिजली पर औसतन खर्च ₹ 180 आता है। यदि विद्युत् उत्पादन का व्यय 20% बढ़ जाए तो प्रति परिवार बिजली का खर्च प्रतिमाह कितने रुपये हो जाएगा?
हल:
2 बल्ब वे 1 पंखा चलाने पर प्रतिमाह बिजली पर औसत खर्च = ₹ 100
विद्युत् उत्पादन के व्यय में वृद्धि = 180 का 20 % = 180 x = ₹ 36
वृद्धि के पश्चात् प्रतिमाह और समान खर्च = 180 + 36 = ₹ 216

अभ्यास 12(h)

प्रश्न 1.
निम्नांकित सारणी में रिक्त स्थानों को अपनी अभ्यास-पुस्तिका में भरिए (भरकर)-
उत्तर-

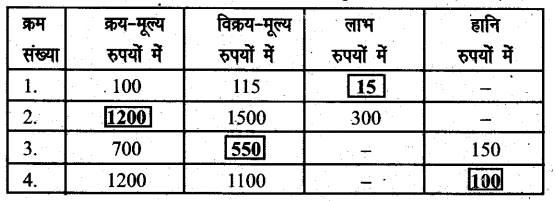
प्रश्न 2.
रहीम ने एक घड़ी में ₹ 1400 में खरीदकर ₹ 1600 में बेच दी। उसे कितना लाभ हुआ?
हल:
घड़ी का क्रय मूल्य = ₹ 1400
घड़ी का विक्रय मूल्य = ₹ 1600
लाभ = विक्रय – क्रय = 1600 – 1400 = ₹ 200

प्रश्न 3.
गीता ने एक साड़ी के 750 में बेची, इसमें ₹ 125 की हानि हुई। साड़ी का क्रय-मूल्य ज्ञात कीजिए।
हल:
साड़ी का विक्रय-मूल्य = ₹ 750
होनि = ₹ 125
साड़ी का क्रय-मूल्य = विक्रय-मूल्य + हानि = 750 + 125 = ₹ 875

प्रश्न 4.
एक किसान ने एक गाय ₹ 1300 में खरीदी और उसे ₹ 250 की हानि उठाकर बेच दी। किसान ने गाय कितने रुपए में बेची?
हल:
गाय का क्रय मूल्य = ₹ 1300
हानि = ₹ 250
गाय का विक्रय मूल्य = क्रय मूल्य – हानि = 1300 – 250 = ₹ 1050

प्रश्न 5.
हरीश ने एक पुरानी स्कूटर ₹ 7000 में खरीदी और ₹ 600 उसकी मरम्मत में खर्च किया। बताइए स्कूटर का लागत मूल्य क्या है?
हल:
स्कूटर का क्रय मूल्य = ₹ 7000
स्कूटर की मरम्मत = ₹ 600
स्कूटर का कुल लागत मूल्य = 7000 + 600 = ₹ 7600

प्रश्न 6.
डेविड ने एक मकान 48000 में खरीदा। उसने उसकी रँगाई-पोताई और साज-सज्जा में ₹ 2000 खर्च किया। उसने उस मकान को ₹ 55000 में बेच दिया। बताइए उसे कितना लाभ हुआ? उत्तर-
मकान का क्रय मूल्य = ₹ 48000
मकान का रँगाई खर्च = ₹ 2000
मकान की लगात = 48000 + 2000 = ₹ 50000
मकान का विक्रय मूल्य = ₹ 55000
लाभ = 55000 – 50000 = ₹ 5000

अभ्यास 12(i)

प्रश्न 1.
निम्नांकित सारणी में जहाँ सम्भव हो रिक्त स्थानों की पूर्ति अपनी अभ्यास पुस्तिका में कीजिए (पूर्ति करके)-

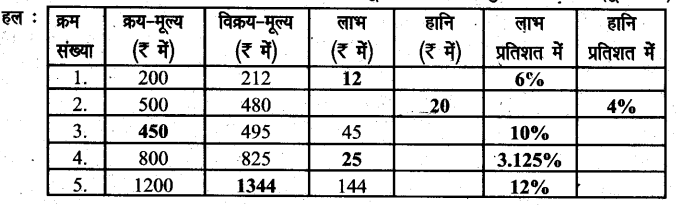
प्रश्न 2.
एक दुकानदार ने एक किताब ₹ 10 में खरीदकर ₹ 11 में बेच दी। कितने प्रतिशत लाभ हुआ?

प्रश्न 3.
एक व्यापारी ने 10 किग्रा घी ₹ 1500 में खरीदकर उसे. ₹ 200 प्रति किंग्रा के भाव में बेच दिया। बताइए उसे कितने प्रतिशत का लाभ हुआ?

प्रश्न 4.
एक हीटर ₹ 180 में खरीदा गया और ₹ 160 में बेचा गया। बताइए कितने प्रतिशत की हानि हुई?

प्रश्न 5.
एक घड़ी ₹ 360 में खरीदी गई तथा 10% लाभ पर बेच दी गई, तो उसका विक्रय मूल्य बताइए।

प्रश्न 6.
रोमेश ने एक मोटरसाइकिलर ₹ 36000 में खरीदी। वह उसे कितने रुपये में बेचें कि 30% का लाभ हो?

प्रश्न 7.
एक टेपरिकार्डर 12% की हानि से ₹ 880 में बेचा गया। उसका क्रय मूल्य ज्ञात कीजिए।

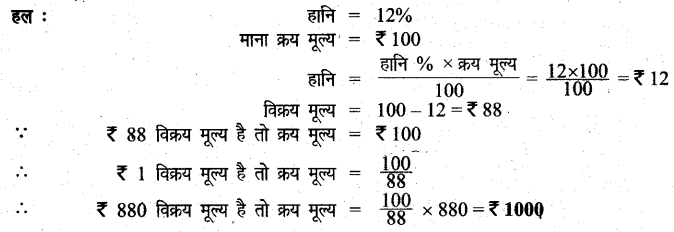
प्रश्न 8.
मोहित ने एक बछड़ा ₹ 2500 में खरीदा और उसे 6% की हानि पर बेच दिया। बछड़े का विक्रय मूल्य ज्ञात कीजिए।

प्रश्न 9.
एक फर्नीचर विक्रेता ने एक सोफासेट 5% लाभ से ₹ 4620 में बेचा। उसका लाभ ज्ञात कीजिए।

प्रश्न 10.
प्रतिशत लाभ या प्रतिशत हानि ज्ञात कीजिए जबकि-

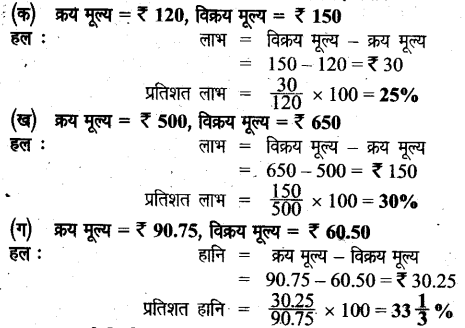
प्रश्न 11.
7 मेजों को ₹ 1288 में बेचने पर 8% की हानि होती है। एक मेज का क्रय मूल्य ज्ञात कीजिए।

प्रश्न 12.
एक फल विक्रेता ने ₹ 10 प्रति दर्जन के भाव से कुछ संतरे खरीदे और ₹ 9 प्रति दर्जन के भाव से बेच दिए। बताइए उसे कितने प्रतिशत की हानि हुई?

प्रश्न 13.
एक व्यक्ति ने 5 दर्जन अण्डे ₹ 12 प्रति दर्जन की दर से खरीदा। उनमें से ₹ 10 अंडे टूट गए और शेष को उसने ₹ 18 प्रति दर्जन के भाव से बेच दिया। उसका प्रतिशत लाभ या हानि ज्ञात कीजिए।

प्रश्न 14.
बताइए निम्न कथनों में कौन सत्य है और कौन असत्य है (बताकर)-

अभ्यास 12(j)

प्रश्न 2.
निम्नलिखित सारणी अपनी अभ्यास पुस्तिका में बनाइए और रिक्त स्थान भरिए (भरकर)-
हल:

प्रश्न 3.
ब्याज की दर बताइए-

प्रश्न 4.
ब्याज की गणना कीजिए।

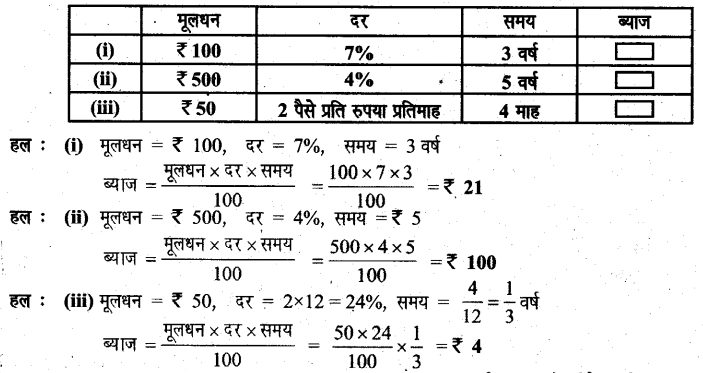
प्रश्न 5.
नीचे दिए गए कोष्ठक के विकल्पों में से सही विकल्प चुनकर खाली स्थान की पूर्ति अपनी अभ्यास पुस्तिका में ही कीजिए – (पूर्ति करके) – [ब्याज, मूलधन, दर, मिश्रधन]
हल:
(क) जो धन उधार दिया या लिया जाता है उसे मूलधन कहते हैं।
(ख) उधार ली गई धनराशि के उपयोग के बदले दी जाने वाली अतिरिक्त राशि को ब्याज कहते हैं।
(ग) मिश्रधन = मूलधन + ब्याज
(घ) मिश्रधन – ब्याज = मूलथन।

प्रश्न 6.
वार्षिक ब्याज दर ज्ञात कीजिए यदि मूलधन = ₹ 100, समय = 1 वर्ष और मिश्रधन = ₹ 107 हो।

प्रश्न 7.
एक किसान ने 12% वार्षिक की दर से ₹ 2,400 उथार लिया। उसने 2वर्ष बाद ₹ 1,200 तथा एक गाय देकर उथार चुका दिया। गाय का मूल्य ज्ञात कीजिए।

प्रश्न 8.
₹ 12.5% वार्षिक ब्याज का क्या अर्थ है? लिखिए।
हल:
12.5% वार्षिक ब्याज का अर्थ है-
₹ 100 पर 1 वर्ष का ब्याज ₹ 12.50 है।

प्रश्न 9.
जार्ज ने एक स्कूल को ₹ 3600 दान दिया। इस दान राशि के ब्याज से समान मूल्य की 6 छात्रवृत्तियाँ, दी जाती हैं। यदि दान की राशि पर 10% वार्षिक ब्याज मिले तो प्रत्येक छात्रवृत्ति का मूल्य ज्ञात कीजिए।

प्रश्न 10.
करीम बाग लगाने के लिए बैंक से ₹ 15000 का ऋण लेता है। बैंक पौधों की खरीद के लिए ऋण का 20% छूट देने के बाद शेष धनराशि पर 9% वार्षिक साधारण ब्याज लेता है। 4 वर्ष बाद, करीम पूरा ऋण अदा करने के लिए बैंक को कितना धन देगा?

प्रश्न 11.
किस वार्षिक साधारण ब्याज की दर से 20 वर्षों में किसी धन का मिश्रधन चार गुना हो जाएगा ?

अभ्यास 12(k)

निम्नांकित प्रश्नों में दिए गए विकल्पों में से सही विकल्प चुनकर रिक्त स्थान भरिए (भरकर)-

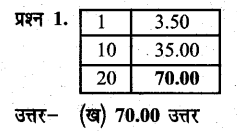
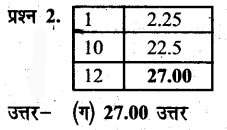
प्रश्न 4.
एक पाठशाला में 175 मीटर टाट ₹ 4.25 प्रति मीटर की दर से खरीदा गया। कुल टाट का मूल्य व्यवहार गणित द्वारा ज्ञात कीजिए।

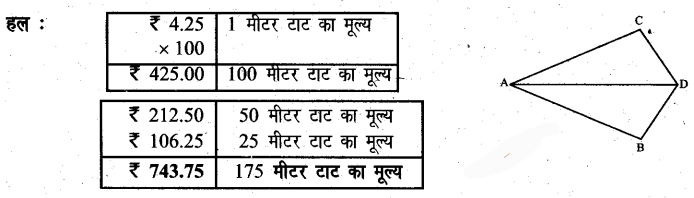
प्रश्न 5.
एक बोरे आलू को भार 79.750 किग्रा है। ऐसे ही 151 बोरे आलू का भार व्यवहार गणित द्वारा निकालिए।

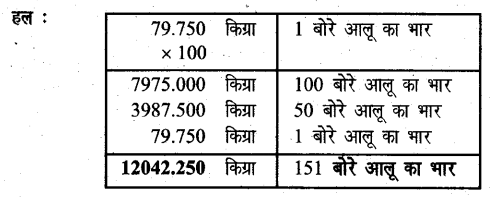
प्रश्न 6.
95 किग्रा चीनी का मूल्य ₹ 16.25 प्रति किग्रा की दर से व्यवहार गणित द्वारा ज्ञात कीजिए।

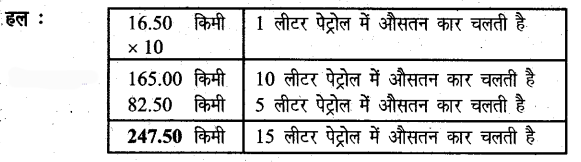
प्रश्न 7.
एक कार 1 लीटर पेट्रोल में 16.50 किमी का औसत देती है। 15 लीटर पेट्रोल में वह कितनी दूर जा सकती है? व्यवहार गणित द्वारा निकालिए।

We hope the UP Board Solutions for Class 6 Maths Chapter 12 वाणिज्य गणित help you. If you have any query regarding UP Board Solutions for Class 6 Maths Chapter 12 वाणिज्य गणित, drop a comment below and we will get back to you at the earliest.