UP Board Solutions for Class 10 Maths Chapter 3 Pairs of Linear Equations in Two Variables
These Solutions are part of UP Board Solutions for Class 10 Maths. Here we have given UP Board Solutions for Class 10 Maths Chapter 3 Pairs of Linear Equations in Two Variables.
प्रश्नावली 3.1 (NCERT Page 49)
प्र. 1. आफ़ताब अपनी पुत्री से कहता है, ‘सात वर्ष पूर्व मैं तुमसे सात गुनी आयु का था | अब से 3 वर्ष बाद मैं तुमसे केवल तीन गुनी आयु का रह जाऊँगा’ (क्या यह मनोरंजक है?) इस स्थिति को बीजगणितीय एवं ग्राफीय रूपों में व्यक्त कीजिए|
हल :
माना आफ़ताब की वर्त्तमान आयु = x वर्ष
और उसकी पुत्री की वर्त्तमान आयु = y वर्ष
7 वर्ष पूर्व आफ़ताब की आयु = x – 7 वर्ष
और उसकी पुत्री की आयु = y – 7 वर्ष
स्थित – I
x – 7 = 7(y – 7)
x – 7 = 7y – 49
x – 7y = 7 – 49
x – 7y = – 42 ……… (1)
3 वर्ष बाद आफ़ताब की आयु = x + 3 वर्ष
और उसकी पुत्री की आयु = y + 3 वर्ष
स्थित – II
x + 3 = 3(y + 3)
x + 3 = 3y + 9
x – 3y = 9 – 3
x – 3y = 6 ……. (2)
बीजगणितीय रूप में :
x – 7y = – 42 ……… (1)
x – 3y = 6 ……. (2)

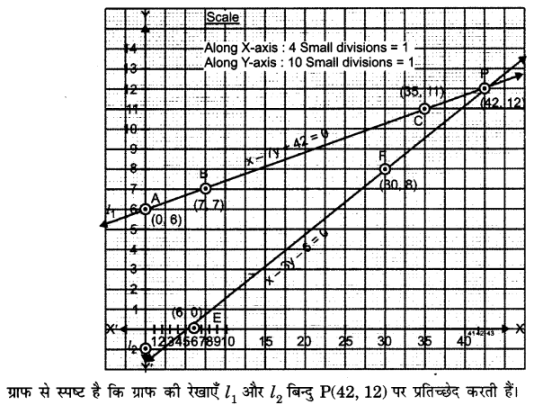
प्र. 2. क्रिकेट टीम के एक कोच ने 3900 रू में 3 बल्ले तथा 6 गेंदे खरीदी बाद में उसने एक और बल्ला तथा उसी प्रकार की 2 गेंदे 1300 रू में खरीदीं इस स्थिति को बीजगणितीय तथा ज्यामितीय रूपों में व्यक्त कीजिए
हल : माना एक बल्ले का मूल्य = x रुपये
और एक गेंद का मूल्य = y रुपये
अत: बीजगणितीय निरूपण
3x + 6y = 3900 ………. (1) और
x + 2y = 1300 ………. (2)
समी० (1) से
3x + 6y = 3900
3(x + 2y) = 3990
या x + 2y = 1300
x = 1300 – 2y
इसी प्रकार समी० (2) से
x + 2y = 1300
x = 1300 – 2y
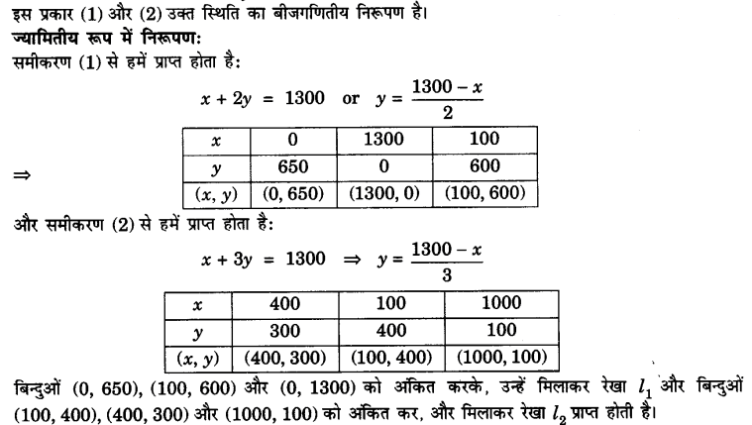

प्र. 3. 2kg सेब और 1 kg अंगूर का मूल्य किसी दिन 160 रू था | एक महीने बाद 4 kg सेब और दो kg अंगूर का मूल्य 300 रू हो जाता है |इस स्थिति को बीजगणितीय तथा ज्यामितीय रूपों में व्यक्त कीजिए
हल : माना एक किलों सेब का मूल्य = x रुपया
और एक किलो अंगूर का मूल्य = y रुपया
अत: बीजगणितीय निरूपण :
2x + y = 160 ……… (1)
4x + 2y = 300 …….. (2)
ग्राफीय निरूपण :
समी० (1) से
2x + y = 160
y = 160 – 2x
अब समी० (2) से
4x + 2y = 300
या 2x + y = 150
y = 150 – 2x


प्रश्नावली 3.2 (NCERT Page 55)
प्र. 1. निम्न समस्याओं में रैखिक समीकरणों के युग्म बनाइए और उनके ग्राफीय विधि से हल ज्ञात कीजिए
(i) कक्षा x के 10 विधार्थियों ने एक गणित की पहेली प्रतियोगिता में भाग लिया यदि लड़कियों की संख्या लड़कों से 4 अधिक हो, तो प्रतियोगिता में भाग लिए लडको और लड़कियों की संख्या ज्ञात कीजिए
हल :
माना लड़कियों की संख्या = x
तथा लड़कों की संख्या = y
प्रश्नानुसार,
लड़के और लडकियाँ की कुल संख्या 10 है|
इसलिए, x + y = 10 …….. (1)
लड़कों से लड़कियाँ 4 अधिक हैं |
इसलिए, x – y = -4 …….. (2)
समी० (1) के लिए तालिका
x + y = 10
⇒ y = 10 – x
समी० (2) के लिए तालिका
x – y = -4
⇒ y = x + 4




ग्राफीय विधि से हल के लिए हम जब बने ग्राफ को देखते हैं तो पाते हैं कि बिंदु (3, 5) दिए गए समीकरण के लिए प्रतिच्छेदन बिंदु है जो कि रैखिक समीकरण युग्म का उभयनिष्ठ हल है |
इसलिए, पेन्सिल का मूल्य = 3 और कलम का मूल्य = 5 है|
प्र 2. अनुपातों ,
और
की तुलना कर ज्ञात कीजिए कि निम्न समीकरण युग्म द्वारा निरूपित रेखाएँ एक बिंदु पर प्रतिच्छेद करती हैं, समांतर हैं अथवा संपाती हैं।
(i) 5x – 4y +8 = 0
7x + 6y – 9 = 0
(ii) 9x +3y + 12 = 0
18x + 6y + 24 = 0
(iii) 6x – 3y + 10 = 0
2x – y + 9 = 0


प्र० 3. अनुपातों ,
और
की तुलना कर ज्ञात कीजिए कि निम्न रैखिक समीकरणों के युग्म संगत हैं या असंगतः
(i) 3x + 2y = 5;
2x – 3y = 7
(ii) 2x – 3y = 8;
4x – 6y = 9
(iii) x –
y = 7;
9x – 10y = 14
(iv) 5x – 3y = 11
-10x + 6y = -22
(v) x + 2y = 8;
2x + 3y = 12

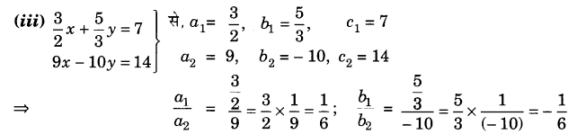

प्र० 4. निम्न रैखिक समीकरणों के युग्मों में से कौन से युग्म संगत /असंगत है, यदि संगत है तो ग्राफीय विधि से हल ज्ञात कीजिए |
(i) x + y = 5, 2x + 2y = 10
(ii) x – y = 8, 3x – 3y = 16
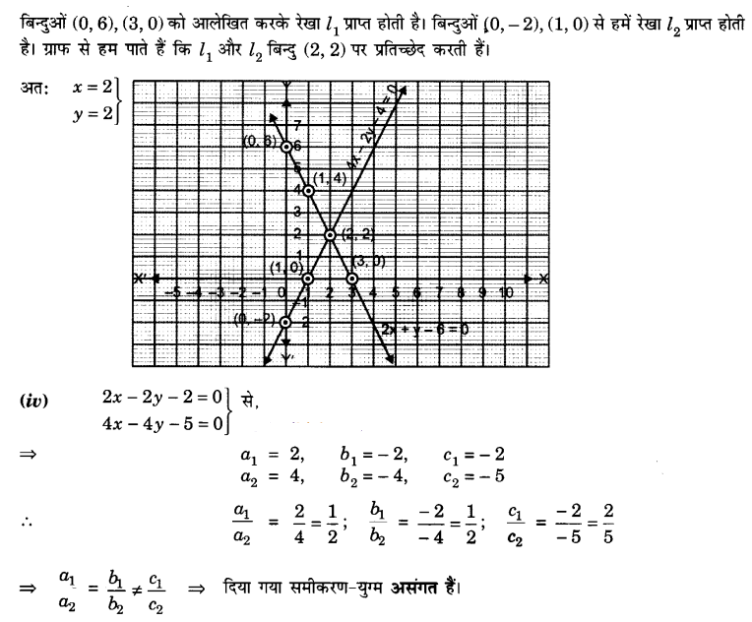
(iii) 2x + y – 6 = 0, 4x – 2y – 4 = 0
(iv) 2x – 2y – 2 = 0, 4x – 4y – 5 = 0

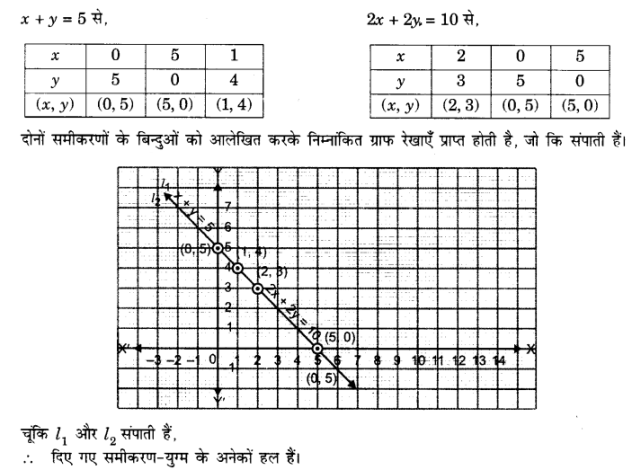

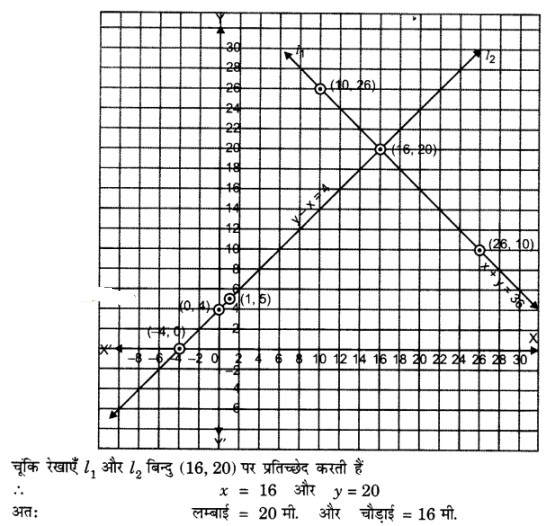
प्र० 5. एक आयताकार बाग़ जिसकी लंम्बाई, चौड़ाई से 4m अधिक है, का अर्धपरिमाप 36m है| बाग़ की विमाएँ ज्ञात कीजिए|
हल : माना आयताकार बाग की लंबाई = x m
और चौड़ाई = y m है|
अर्धपरिमाप = 36 m

प्र० 6. एक रैखिक समीकरण 2x + 3y – 8 = 0 दी गई है दी चरों में एक ऐसी और रैखिक समीकरण लिखिए ताकि प्राप्त युग्म का ज्यामितीय निरूपण जैसा कि
(i) प्रतिछेद करती रेखाएँ हों
(ii) समांतर रेखाएँ हों|
(iii) संपाती रेखाएँ हों
हल : 2x + 3y – 8 = 0 …… (i) (दिया है)
हमें एक और ऐसी ही रैखिक समीकरण खींचना है जिससे प्राप्त युग्म का ज्यामितीय निरूपण
(i) प्रतिच्छेद करती रेखाए हो
रेखाए प्रतिच्छेद करती हो इसके लिए

प्र० 7. समीकरणों x – y + 1 = 0 और 3x + 2y – 12 = 0 का ग्राफ खींचिए x- अक्ष और इन रेखाओं से बने त्रिभुज के शीर्षों के निर्देशक ज्ञात कीजिए और त्रिभुजाकार पटल को छायांकित कीजिए

प्रश्नावली 3.3 (NCERT Page 59)
प्र० 1. निम्न रैखिक समीकरण युग्म को प्रतिस्थापन विधि से हल कीजिए :



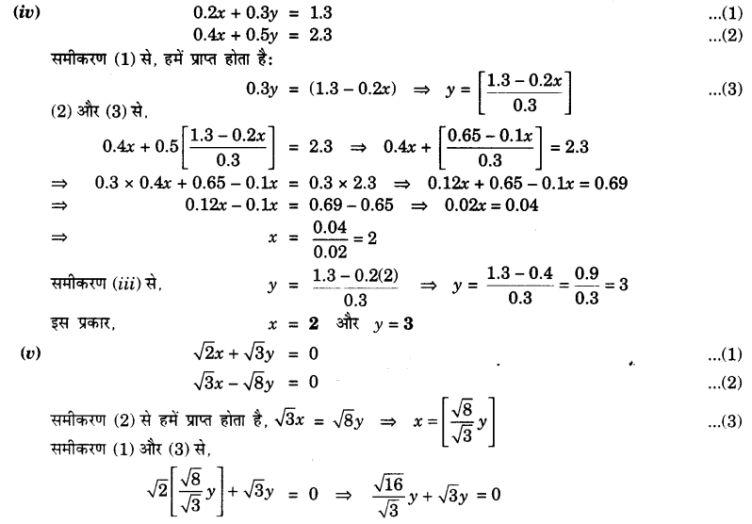
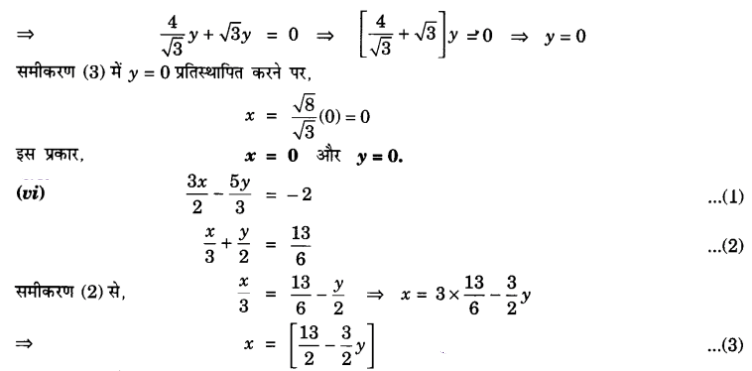

प्र० 2. 2x + 3y = 11 और 2x – 4y = -24 को हल कीजिए और इसमें ‘m’ का वह मान ज्ञात कीजिए जिसके लिए y = mx + 3 हो |
हल :
2x + 3y = 11 ……. (i)
2x – 4y = – 24 ….. (ii)
समीकरण (i) से
2x + 3y = 11

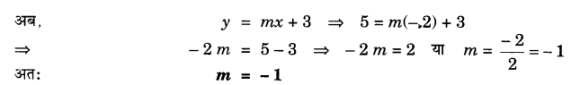
प्र 3. निम्न समस्याओं में रैखिक समीकरण युग्म बनाइए और उनके हल प्रतिस्थापन विधि द्वारा ज्ञात कीजिए।
(i) दो संख्याओं का अंतर 26 है और एक संख्या दूसरी संख्या की तीन गुनी है। उन्हें ज्ञात कीजिए।
(ii) दो संपूरक कोणों में बड़ा कोण छोटे कोण से 18 डिग्री अधिक है। उन्हें ज्ञात कीजिए।
(iii) एक क्रिकेट टीम के कोच ने 7 बल्ले तथा 6 गेंदें 3800 में खरीदीं। बाद में, उसने 3 बल्ले तथा 5 गेंदें 1750 में खरीदी। प्रत्येक बल्ले और प्रत्येक गेंद का मूल्य ज्ञात कीजिए।
(iv) एक नगर में टैक्सी के भाड़े में एक नियत भाड़े के अतिरिक्त चली गई दूरी पर भाड़ा सम्मिलित किया जाता है। 10 किमी. दूरी के लिए भाड़ा 105 है तथा 15 किमी. के लिए भाड़ा 155 है। नियत भाड़ा तथा
प्रति किमी. भाड़ा क्या है? एक व्यक्ति को 25 किमी. यात्रा करने के लिए कितना भाड़ा देना होगा?
(v) यदि किसी भिन्न के अंश और हर दोनों में 2 जोड़ दिया जाए, तो वह हो जाती है। यदि अंश और हर दोनों में 3 जोड़ दिया जाए, तो वह
हो जाती है। वह भिन्न ज्ञात कीजिए।
(vi) पाँच वर्ष बाद जैकब की आयु उसके पुत्र की आयु से तीन गुनी हो जाएगी। पाँच वर्ष पूर्व जैकब की आयु उसके पुत्र की आयु की सात गुनी थी। उनकी वर्तमान आयु क्या है?







प्रश्नावली 3.4 (NCERT Page 63)
प्र 1. निम्न समीकरणों के युग्म को विलोपन विधि तथा प्रतिस्थापना विधि से हल कीजिए कौन सी विधि अधिक उपयुक्त है ?
(i) x + y = 5 और 2x – 3y = 4
(ii) 3x + 4y = 10 और 2x – 2y = 2
(iii) 3x – 5y – 4 = 0 और 9x = 2y + 7
(iv) +
= -1 और x –
= 3




प्र 2. निम्न समस्याओं में रैखिक समीकरणों के युग्म बनाइए और उनके हल (यदि उनका अस्तित्व हो) विलोपन विधि से ज्ञात कीजिए:
(i) यदि हम अंश में 1 जोड़ दें तथा हर में से 1 घटा दें, तो भिन्न 1 में बदल जाती है। यदि हर में 1 जोड़ दें, तो यह हो जाती है। यह भिन्न क्या है?
(ii) पाँच वर्ष पूर्व नूरी की आयु सोनू की आयु की तीन गुनी थी। दस वर्ष पश्चात्, नूरी की आयु सोनू की आयु की दो गुनी हो जाएगी। नूरी और सोनू की आयु कितनी है?
(iii) दो अंकों की संख्या के अंकों का योग 9 है। इस संख्या का नौ गुना, संख्या के अंकों को पलटने से बनी संख्या का दो गुना है। वह संख्या ज्ञात कीजिए।
(iv) मीना 2000 निकालने के लिए एक बैंक गई। उसने खजाँची से रे 50 तथा 100 के नोट देने के लिए कहा। मीना ने कुल 25 नोट प्राप्त किए। ज्ञात कीजिए कि उसने 50 और 100 के कितने-कितने नोट प्राप्त किए।
(v) किराए पर पुस्तकें देने वाले किसी पुस्तकालय का प्रथम तीन दिनों का एक नियत किराया है तथा उसके बाद प्रत्येक अतिरिक्त दिन का अलग किराया है। सरिता ने सात दिनों तक एक पुस्तक रखने के लिए 27 अदा किए, जबकि सूसी ने एक पुस्तक पाँच दिनों तक रखने के 21 अदा किए। नियत किराया तथा प्रत्येक अतिरिक्त दिन का किराया ज्ञात कीजिए।
हलः
(i) माना भिन्न का अंश = x और भिन्न का हर =y







प्रश्नावली 3.5 (NCERT Page 69)
प्र 1. निम्न रैखिक समीकरणों के युग्मो में से किसका एक अद्दितीय हल है, किसका कोई हल नहीं हा या किसके अपरिमित रूप से अनेक हल है | अद्दितीय हल की स्थिति में, उसे ब्रज – गुणन विधि से ज्ञात कीजिए
(i) x – 3y = 0
3x – 9y – 2 = 0
(ii) 2x + y = 5
3x + 2y = 8
(iii) 3x – 5y = 20
6x – 10y = 40
(iv) x – 3y – 7 = 0
3x – 3y – 15 = 0


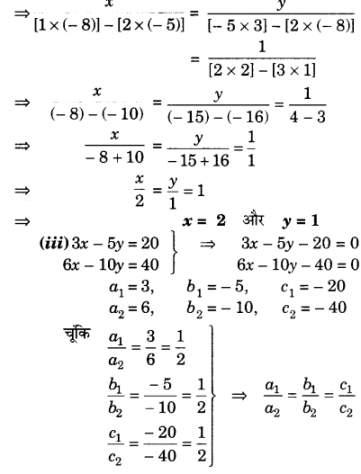


प्र 2. (i) a और b के किन मानों के लिए, रैखिक समीकरणों के युग्म के अपरिमित रूप से अनेक हल होंगे?
2x + 3y = 7
(a – b) x + ( a + b) y = 3a + b – 2
(ii) k के किस मान के लिए, निम्न रैखिक समीकरणों के युग्म का कोई हल नहीं है ?
3x + y = 1
(2k – 1) x + (k – 1) y = 2k + 1
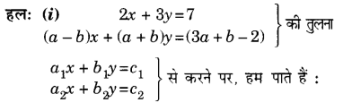



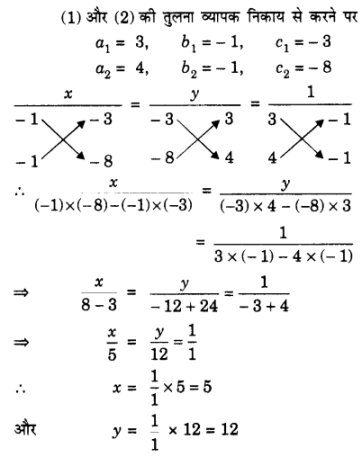
प्र 3. निम्न रैखिक समीकरणों के युग्म को प्रतिस्थापन एंव व्रज – गुणन विधियों से हल कीजिए किस विधि को आप अधिक उपयुक्त मानते हैं ?
8x + 5y = 9
3x + 2y = 4



प्र 4. निम्न समस्याओं में रैखिक समीकरणों के युग्म बनाइए और उनके हल (यदि उनका अस्तित्व हो) किसी बीजगणितीय विधि से ज्ञात कीजिए :
(i) एक छात्रावास के मासिक व्यय का एक भाग नियत है तथा शेष इस पर निर्भर करता है कि छात्र ने कितने दिन भोजन लिया है| जब एक विद्धार्थी A को, जो 20 दिन भोजन करता है, 1000 रू छात्रावास के व्यय के लिए अदा करने पड़ते है, जबकि एक विधार्थी B को,जो 26 दिन भोजन करता है छात्रावास के व्यय के लिए 1180 रू अदा करने पड़ते है | नियत व्यय और प्रतिदिन के भोजन का मूल्य ज्ञात कीजिए|
(ii) एक भिन्न हो जाती है, जब उसके अंश से 1 घटाया जाता है और वह
हो जाती है जब हर में 8 जोड़ दिया जाता है| वह भिन्न ज्ञात कीजिए|
(iii) यश ने एक टेस्ट में 40 अंक अर्जित किए, जब उसे प्रत्येक सही उत्तर पर 3 अंक मिले तथा अशुद्ध उत्तर पर 1 अंक की कटौती की गई | यदि उसे सही उत्तर पर 4 अंक मिलते तथा अशुद्ध उत्तर पर 2 अंक कटते, तो यश ५०अन्क अर्जित करता टेस्ट में कितने प्रश्न थे ?
(iv) एक राजमार्ग पर दो स्थान A और B, 100 km की दुरी पर है | एक कार A से तथा दूसरी कार b से एक ही समय चलना प्रारम्भ करती है | यदि ए कारे भिन्न भिन्न चालों से एक ही दिशा में चलती है, तो वे 5 घंटे पश्चात् मिलती हैं | दोनों कारों की चाल ज्ञात कीजिए|
(v) एक आयात का क्षेत्रफल 9 वर्ग इकाई कम हो जाता है, यदि उसकी लंबाई 5 इकाई कम कर दी जाती है और चौड़ाई 3 इकाई बढ़ा दी जाती है| यदि हम लंबाई को 3 इकाई और चौड़ाई को 2 इकाई बढ़ा दे, तो क्षेत्रफल 67 वर्ग इकाई बढ़ जाता है| आयत की विमाएँ ज्ञात कीजिए|








प्रश्नावली 3.6 (NCERT Page 74)
प्र 1. निम्न समीकरणों के युग्मों को रैखिक समीकरणों के युग्म में बदल करके हल कीजिए :
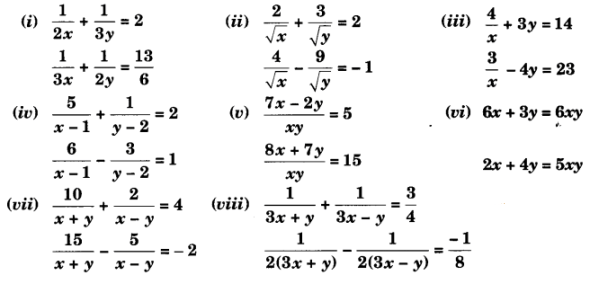















प्र 2. निम्न समस्याओं को रैखिक समीकरण युग्म के रूप में व्यक्त कीजिए और फिर उनके हल ज्ञात कीजिए :
(i) रितु धारा के अनुकूल 2 घंटे में 20 km तैर सकती है और धारा के प्रतिकूल 2 घंटे में 4 km तैर सकती है| उसकी स्थिर जल में तैरने की चाल तथा धारा की चाल ज्ञात कीजिए|
(ii) 2 महिलाएँ एंव 5 पुरुष एक कसीदे के काम को साथ- साथ 4 दिन में पूरा कर सकते है | जबकि 3 महिलाएँ एंव 6 पुरुष इसको 3 दिन में पूरा कर सकते है ज्ञात कीजिए कि इसी कार्य को करने में एक महिला कितना समय लेगी | पुनः इसी कार्य को करने में एक पुरुष कितना समय लेगा|
(iii) रूही 300 km दुरी पर स्थित अपने घर जाने के लिए कुछ दुरी रेलगाड़ी द्वारा तथा कुछ दुरी बस द्वारा तय करती है | यदि वह 60 km रेलगाड़ी द्वारा तथा शेष बस द्वारा यात्रा करती है तो उसे 4 घंटे लगते हैं | यदि वह 100 km रेलगाड़ी से तथा शेष बस से यात्रा करे, तो उसे 10 मिनट अधिक लगते हैं| रेलगाड़ी एंव बस की क्रमशः चाल ज्ञात कीजिए|





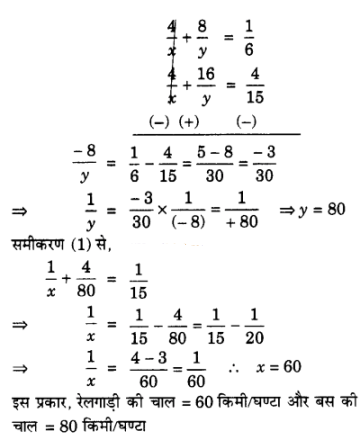
प्रश्नावली 3.7 (NCERT Page 75)
प्र 1. दो मित्रों अनी और बीजू की आयु में 3 वर्ष का अन्तर है| अणि के पिता धरम की आयु अणि की आयु की दुगुनी और बीजू की आयु अपनी बहन कैथी की आयु की दुगुनी है| कैथी और धरम की आयु का अन्तर 300 वर्ष है| अणि और बीजू की आयु ज्ञात कीजिए|


प्र 2. एक मित्र दूसरे से कहता है कि ‘यदि मुझे एक सौ दे दो, तो मैं आपसे दो गुना धनी बन जाऊँगा’ दूसरा उत्तर देता है ‘यदि आप मुझे दस दे दें, तो मैं आपसे छः गुना धनी बन जाऊँगा|’ बताइए की उनकी क्रमशः कल्या संपत्तिया हैं ?

प्र 3. एक रेलगाड़ी कुछ दूरी समान चाल से तय करती है | यदि रेलगाड़ी 10 km/h अधिक तेज चलती होती, तो उसे नियत समय से 2 घंटे कम लगते और यदि रेलगाड़ी 10 km/h धीमी चलती होती, तो उसे नियत समय से 3 घंटे अधिक लगते | रेलगाड़ी द्वारा तय की गई दुरी ज्ञात कीजिए|


प्र 4. एक कक्षा के विधार्थियों को पंक्तियों में खड़ा होना है| यदि पंक्ति में 3 विधार्थी अधिक होते, तो पंक्ति कम होती| यदि पंक्ति में 3 विधार्थी कम होते, तो 2 पंक्तियाँ अधिक बनतीं| कक्षा में विधार्थियों की संख्या ज्ञात कीजिए|



प्र 5. एक त्रिभुज ∆ABC में, ∠C = 3 ∠B = 2(∠A + ∠B) है| त्रिभुज के तीनों कोण ज्ञात कीजिए|


प्र 6. समीकरणों 5x – y = 5 और 3x – y = 3 के ग्राफ खींचिए| इन रेखाओं और y -अक्ष से बने त्रिभुज के शीर्षों के निर्देशांक ज्ञात कीजिए| इस प्रकार बने त्रिभुज के क्षेत्रफल का परिकलन कीजिए|


प्र 7. निम्न रैखिक समीकरणों के युग्मों को हल कीजिए :
(i) px + qy = p – q
qx – pq = p + q
(ii) ax + by = c
bx + ay = 1 + c
(iii) –
= 0
ax + by = a² + b²
(iv) (a – b) x + (a + b) y = a² – 2ab – b²
(a + b) (x + y ) = a² + b²
(v) 152x – 378y = -74
-378x + 152y = -604






प्र 8. ABCD एक चतुर्भुज है इस चक्रीय चतुर्भुज के कोण ज्ञात कीजिए|

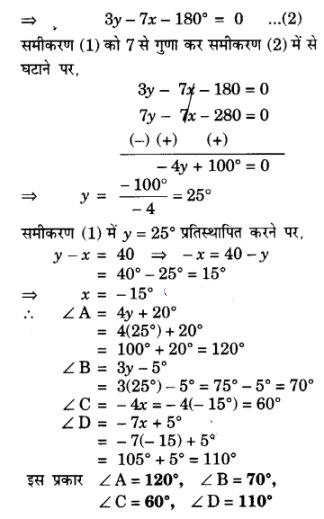
Hope given UP Board Solutions for Class 10 Maths Chapter 3 are helpful to complete your homework.
If you have any doubts, please comment below. UP Board Solutions try to provide online tutoring for you.
One Response
Tenth